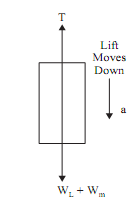
Determine tension in the rope:

An elevator cage of mineshaft, weighing 8KN when, is lifted or lowered by means of wire rope. Once man weighing 600N entered it and lowered with the uniform acceleration such that when the distance of 187.5m was covered, velocity of cage was 25m/sec. determine tension in the rope and the force exerted by man on the floor of cage.

Sol: Given data;

Weight of empty lift W_L  = 8KN = 8000N

Weight of man W_m  = 600N

Distance covered by lift s = 187.5m

Velocity of lift after 187.5m v = 25m/sec

Tension in rope T = ?

Force exerted on man Fm  =?

Apply the relation v²  = u²  + 2as, for finding acceleration

(25)² =0 + 2a (187.5) a =1.67m/sec²                                                                           ...(i)

Cage moves down only when W_L + W_m  >T

Net accelerating force = (W_L  + W_m)- T

Using the relation F = ma, then (W_L + W_m)- T = ma = [(W_L + W_m)/g]a(8000 + 600) - T = [(8000+ 600)/9.81] X 1.67

T = 7135.98N                                                   .......ANS

Calculation for the force exerted by the man. Consider the weight of man only, F_m - W_m = maF_m  - 600 = (600/9.81) X 1.67F_m  = 714.37N

As Newton's third law states that the force of action and reaction between interacting bodies are equal in magnitude but opposite in direction and have the same line of action.

That is, Force exerted by the man = F = 714.37N                                        ........ANS