Determine and classify all the critical points of the given function.  Described the intervals where function is increasing & decreasing.

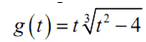
Solution: Firstly we'll require the derivative therefore we can get our hands on the critical points.  Note that we'll do some simplification on the derivative to help us find out the critical points.

g ′ (t ) = (t ² - 4)^(1/3)  +(2/3) t ² (t ² - 4)- 3

=(t ² - 4)³  +     2t² / 3(t ² - 4)^(2/3)

=3 (t ² - 4) + 2t ² /3(t ² - 4)^(2/3)

 =5t 2  -12 /3 (t ² - 4)³

Thus, it looks like we'll have four critical points here. They are following,

t =± 2                                      here, the derivative doesn't exist.

t = ±√(12/5) = ±1.549             here, the derivative is zero here.

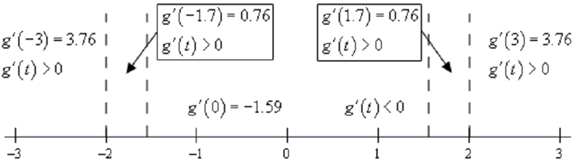
Determining the intervals of increasing & decreasing will also give the classification of the critical points thus let's get those first.  Given is a number line along with the critical points graphed & test points.

Thus, we've got the given intervals of increasing & decreasing.

Increase : - ∞ < x - 2, - 2 < x < -√(12/5) , √(12/5) < x < 2,  &  2 < x < ∞

Decrease :  -√(12/5)

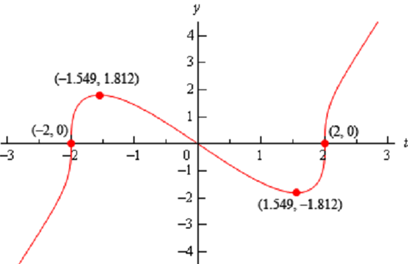
From this it looks like t = -2 & t = 2 are neither relative minimum or relative maximums as the function is increasing on both side of them.  Alternatively, t < -12   is a relative maximum and t =12 is a relative minimum.

Here is the graph of the function.