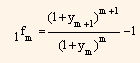Using details from table 8, let us compute the 6-month forward rate. Simple arbitrage principle, like the one used to compute the spot rates are used in this process.

For example, let us consider an investor who has 1-year investment horizon and has two alternatives, (i) to buy a 1-year T-bill or (ii) to buy a 6-month T-bill; and when it matures after six months to buy one more 6-month T-bill. If both investments have the same cash flows and carry the same risk, then they will have same value. The investor will be indifferent towards the two alternatives if both of them produce same returns in the 1-year investment horizon. But, to compare both the options, the investor needs to know the forward rate on the 6-month Treasury bill to calculate the yield available on a 6-month treasury bill that will be purchased six months from now. Using the 6-month and 1-year Treasury bill spot rate, the six month forward rate on a 6-month treasury bill can be equated.

Let us now see how to determine the forward rate. Assume that an investor purchases a six month T-bill for $X. The value of the investment at the end of six months would be:

         X (1 + y₁)

Where,

         y₁ = One-half the Bond-Equivalent Yield (BEY) of the theoretical
            6-month spot rate.

Let us say f represents one-half the forward rate on a 6-month treasury bill available six months from now. The future returns that the investor would be receiving on his investment one year from now if he reinvests his investment by purchasing a six month treasury bill at the end of first six months, would be:

         X (1 + y₁) (1 + f)

If we consider the alternative investment in 1-year T-bill and we assume that y₂ represents one-half the BEY of the theoretical 1-year spot rate, then the total value of the investment at the end of one year would be:

         X (1 + y₂)²

We know that the investor will be indifferent towards the two alternatives if he receives the same return. We can represent it with the help of following equations,

         X (1 + y₁) (1 + f) = X (1 + y₂)²

Solving for f,

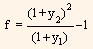
Now using the theoretical spot rates given in table 8, the 6-month and the 1-year
T-bill spot rate would be:

6-month bill spot rate = 0.0400, so y₁ = $1.0200.

1-year bill spot rate = 0.0420, so y₂ = $0.0210.

Substituting the values in equation (1) we get:

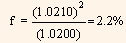
So, the six month forward rate six months form now will be 4.4% (2.2% x 2) BEY. Now let us verify the values determined.  If $X is invested in the 6-month T-Bill at 2% and the proceeds are then reinvested for six months at the 6-month forward rate of 2.2% then the total return form this option would be,

         X(1.0200) x (1.0220) = 1.04244X

Now, if we invest the same amount i.e., $X in 1-year T-bill at one half the
1-year rate, 1.02105%, then return from this option would be,

         X (1.0210)² = 1.04244 X

In a similar manner, 6 month forward rate beginning at any time period in the future can be calculated.  The notation we use to indicate 6-month forward rates is ₁f_m. In this, sub script 1 represents a 1-period (6-month) rate and subscript m represents the period beginning m period form now. When m is zero, then it represents current rate. Therefore, the first six months forward (₁f_m) rate is simply the current six month forward rate (y₁).  The formula to determine a six month forward rate is: