A graph G might be defined as a finite set V of vertices & a set E of edges (pair of connected vertices). The notation utilized is as follows:

Graph G = (V, E)

Consider the graph of Figure

For the graph , the set of vertices is V = {1, 2, 3, 4, 5}.

For the graph ,the set of edges is E = {(1,2), (1,5), (1,3), (5,4), (4,3), (2,3) }.

The elements of E are always a pair of elements.

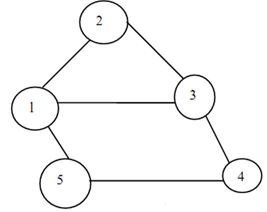
Figure: A graph

It might be noted that unlike nodes of a tree, graph contain a very restricted relationship among the nodes (vertices). There is no direct relationship among the vertices 1 & 4 although they are connected through 3.

Directed graph & Undirected graph: If in a graph every edge (a,b) is marked through a direction from a to b, then we call it a Directed graph (digraph). Conversely, if directions are not marked onto the edges, then the graph is called an Undirected graph.

In a Directed graph, the edges (1,5) & (5,1) represent two distinct edges while in an Undirected graph, (1,5) & (5,1) represent the similar edge. Graphs are utilized in several types of modeling. For instance, graphs can be utilized to represent connecting roads among cities.