DDA or Digital Differential Analyzer Algorithm - Line generation algorithms
From the above discussion we get that a Line drawing is accomplished through calculating intermediate point coordinates along the line path among two specified end points. Because screen pixels are referred along with integer values or plotted positions that may only estimated the calculated coordinates that is pixels that are intensified are those that lie very close to the line path if not accurately on the line path that in this case are exactly horizontal, vertical or 45° lines only. Standard algorithms are available to find out that pixels give the best estimation to the desired line; one that algorithm is the DDA that is Digital Differential Analyzer; algorithm. For the further details of the algorithm, let us discuss several common appearances of the line segment, since the respective appearance decides that pixels are to be intensified. This is also obvious as only such pixels which lie extremely close to the line path are to be intensified since they are the ones that best estimated the line. Apart from the precise situation of the line path, that in this case is exactly horizontal, vertical or 45° lines that is slope zero, infinite or one only. We may also face a situation where the slope of the line is greater than 1 or less then 1.Which is the case shown in following figure.
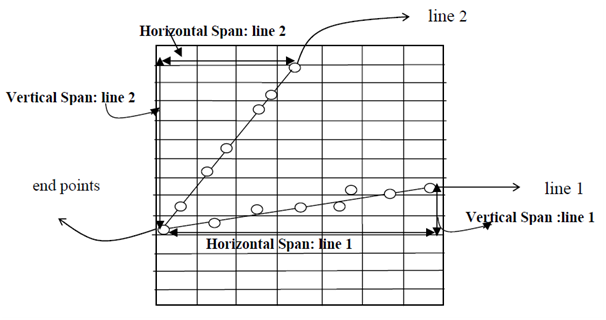
Figure: DDA line generation
A mention in figure there are two lines, Line 1 i.e. slope<1 and line 2 i.e. slope>1. According to the discussion, the common mechanism of construction of these two lines all along with the Digital Differential Analyzer algorithm. Since the slope of the line is a crucial factor in its construction, so let us identify the algorithm in two cases depending upon the slope of the line where it is > 1 or < 1.
Case 1: slope (m) of line is < 1 that is line 1: In this condition to plot the lines we should move the direction of pixel in x via 1 unit all time and after that hunt for the pixel value of the y direction that best suits the line and lighten which pixel in order to plot the line. Hence in Case 1: that is 0 < m < 1 whether x is to be increased then via 1 unit all time and exact y is approximated.
Case 2: slope (m) of line is > 1 that is line 2; if m > 1 that is condition of line 2, then the most suitable strategy would be to move towards the y direction via 1 unit all time and find out the pixel in x direction that best suits the line and acquire which pixel lightened to plot the line. Hence in Case 2: infinity > m > 1 whether y is to be increased via 1 unit every time and exact x is approximated.