Damped free vibrations can be modelled by considering a block of mass m that is attached to a spring and a dashpot as shown.

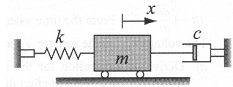
From Newton's second law of motion, the displacement x of the mass as a function of time can be determined by solving the differential equation:

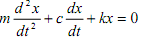
where k is the spring constant, and c is the damping coefficient of the dashpot. If the mass is displaced from its equilibrium position and then released, it will start oscillating back and forth. The nature of the oscillations depends on the size of the mass and the values of k and c.

(a) Create a MATLAB script file that calls for input of m, k, c, and xo. This file calls at least two functions i.e. function (b) that calculate x and v, and function (c) that animates the mass motion.

(b) Create a function M-file that calculates the displacement x and the velocity v of the mass, as function of time, t.

(c) Create another function M-file to create the animation of the mass motion.

(d) Demonstrate the program for two cases: 

(i) c = 3 N-s/m for 0 ≤ t ≤ 20s

(ii) c = 50 N-s/m for 0 ≤ t ≤ 10s

For the system shown in the figure m = 10kg, and k = 28 N/m. At time t = 0 the mass is  displaced to x = 0.18m, and then released from rest.

(e) Write a report describing your programs developed in (a), (b), and (c), and comment on your observation of the results from the two cases in (d).