CONSERVATION OF ENERGY

1.   Potential energy is, as the word suggests, the energy "locked up" up somewhere and which can perform work. Potential energy Potential energy can be converted into kinetic energy, 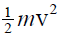  . As I showed you earlier, this follows directly from Newton's laws.

2. If you lift a stone of mass m from the ground up a distance x, you have to do work against gravity. The (constant) force is mg , and so W = mgx. By conservation of energy, the work done by you was transformed into gravitational potential energy whose values is exactly equal to mgx. Where is the energy stored? Answer: it is stored neither in the mass or in the earth - it is stored in the gravitational field of the combined system of stone+earth.

3.  Suppose you pull on a spring and stretch it by an amount x away from its normal (equilibrium) position. How much energy is stored in the spring? Obviously, the spring gets harder and harder to pull as it becomes longer. When it is extended by length x and you pull it a further distance dx, the small amount of work done is dW = Fdx = kxdx. Adding up all the small bits of work gives the total work:

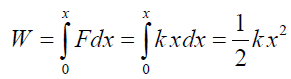
This is the work you did. Maybe you got tired working so hard. What was the result of your working so hard? Answer: this work was transformed into energy stored in the spring. The spring contains energy exactly equal to .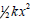

4. Kinetic energy obviously depends on the frame you choose to measure it in. If you are running with a ball, it has zero kinetic energy with respect to you. But someone who is standing will see that it has kinetic energy! Now consider the following situation: a box of mass 12kg is pushed with a constant force so that so that its speed goes from zero to 1.5m/sec (as measured by the person at rest on the cart) and it covers a distance of 2.4m.

Assume there is no friction.