Concept Of Permutation Network
In permutation interconnection networks the information replace requires data transfer from input set of nodes to output set of nodes and likely connections among edges are established by applying a variety of permutations in available links. There are a variety of networks where multiple paths from source to destination are feasible. For finding out what the feasible routes in such networks are the learning of the permutation theory is a must.
Let us see, the basic concepts of permutation with respect to interconnection network. Let us say the network has place of n input nodes and n output nodes.
Permutation P for a network of 5 nodes (i.e., n = 5) is written as follows:
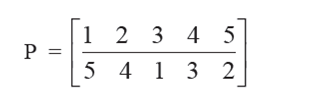
It means that node connections are 1↔5, 2↔ 4, 3↔1, 4↔3, 5↔2.
The connections are shown in the Figure .
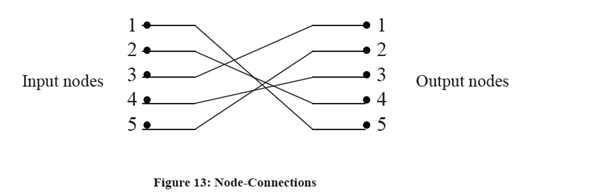

In these examples, only one set of links exist among input and output nodes and means it is a one stage network. It may be possible that there exist many links among input and output (i.e. multistage network). Permutation of all these in a multistage network are known permutation group and these are represented by a cycle e.g. permutation
P= (1,2,3) (4,5) means the network has two sets of input and output nodes, one set consists of nodes 1,2,3 and another group exists of nodes 4,5 and connections are 1→2, 2→3, 3→1, and 4→5. Here set (1,2,3) has period 3 and (4,5) has period 2, collectively these sets has periodicity 3×2=6.
Interconnection from all the feasible input nodes to all the output nodes figured the permutation group.
The permutations can be combined. This is called composition operation. In composition operation more than two permutations are applied in sequence, e.g. if P1 and P2 are two permutations defined as:
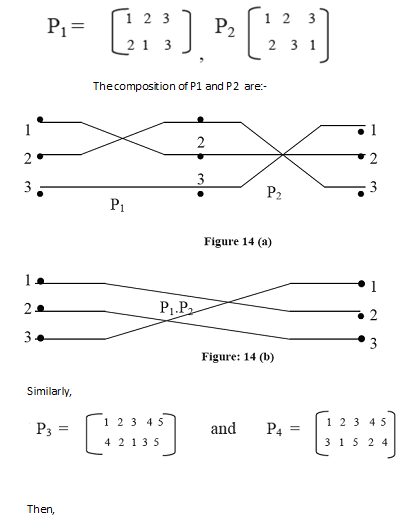
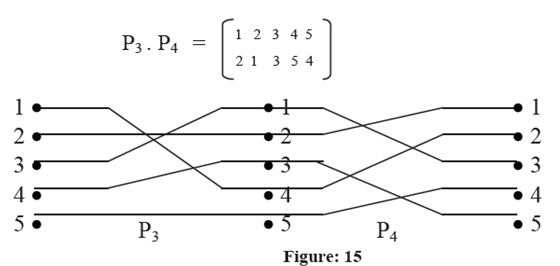
Composition of those permutations P1 P2 are characterized in Figures 14 (a) and 14 (b).There are some permutations of special significance in interconnection network. These permutations are given by hardware. Now, let us talk about these permutations in detail.