Let us consider a situation wherein a position in an interest rate dependent asset such as a bond portfolio or a money market security is hedged by using an interest rate futures contract.

Let us assume that the change in the yield ?y, will be same for all maturities, i.e., only parallel shifts in the yield curve can occur. From the modified duration definition, we have,

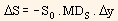
We can also say that to a reasonable approximation, it is also true that,

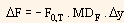
In the first equation, S₀ represents value (decimal form) of the asset that is being hedged and MD_S  represents modified duration of the asset. In the second equation, F_0,T represents quoted price in decimals for the interest rate futures contract and MD_F  represents modified duration of the asset underlying the futures contract (i.e., modified  duration of the cheapest to deliver bond).

As ?y is assumed to be the same for all maturities, we have ρ_ΔSΔF = 1.  By combining first and second equation, we get,

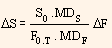
This can be written as,

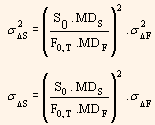
Thus, we get,  

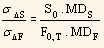
Finally, the optimal Hedge Ratio (HR) is used for hedging 

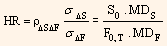
By using this equation we can equate the duration of the combined position equal to zero.

However, the hedge obtained using the above equation is not perfect because of following reasons:

• It assumes that ?y is same for all yields. But, in reality short-term yields are generally more volatile and also have low correlation with long-term yields. Consequently, the performance of the hedge will not be appreciable, particularly when there is large variation between MD_S and MD_F.

• It does not consider convexity. In case the convexity of the asset underlying the futures contract is remarkably different from the convexity of the asset being hedged, and at the same time if there is large difference in interest rates, then the performance hedge will be worse than is expected.

• An assumption with regard to cheapest-to-deliver bond is essential to compute MD_F. If the cheapest-to-deliver bond changes, then MD_F   as well as optimal number of contracts also changes_.

Now, as we know the hedge ratio, let us see the number of futures contracts to be purchased. We have earlier studied that the number of futures contracts required is given as

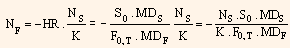
In the above equation, N_S indicates the number of units of spot asset to be hedged and k indicates the contract size.

We can estimate hedge ratio by using regression also. It can be interpreted as follows:

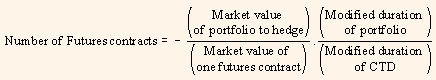
We have earlier studied that,     Here     represents conversion factor of the cheapest to deliver bond at time 0 and S_CTD,0  represents its price. If we replace F_0,T in the above formula, we get,

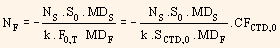
This can be interpreted as follows: