Compute the intensity of normal stress:

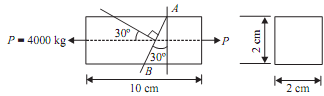
A uniform steel bar of 2 cm × 2 cm area of cross section is subjected to axial pull of 40000 kg. Compute the intensity of normal stress, shear stress and resultant stress on plane normal to which is inclined at 30° to axis of bar. Solve problem graphically by drawing Mohr Circle.

Sol.: Given that:

Load applied 'P'= 4000 × 9.8 = 39.2 kN
σ_x= 39.2/(2 × 10-2)₂  

= 98MN/m²
 
Steps to draw Mohr's circle.

Step1: Take the origin O and draw a horizontal line OX.

Step2: The cut off OA equal to σ_x by taking the scale

1 mm = 1MN/m²
 
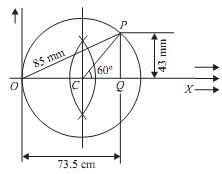
Step 3: Bisect OA at point C

Step 4: Having C as centre and radius CA draw circle.

Step 5: At point C draw a line CP at an angle 2θ with OX meeting circle. At point P (θ is angle made by oblique plane with the minor principle stress, here zero).

Step 6: Through point P draw perpendicular to OX, it intersect OX at point Q, join OP. Measure OQ, PQ and OQ as σ, τ and σ_r respectively. Thus;

Normal stress on plane σ = OQ = 73.5 × 1 = 73.5MN/m²

Tangential or shear stress on plane τ = PQ = 43 × 1 = 43 MN/m²

And Resultant stress σ_r = OP = 85 × 1 = 85 MN/m².