Compare the probabilities:

Use the central limit theorem to compute P (¦ X - μ ¦ ≥ k), k = 1, 2,3,4,5 where X and μ are as defined in Example. Compare the probabilities with the probabilities computed in Example.

Solution:

We have np = 2, npq = 1, n = 4 and so

P(¦X - μ¦≥ k)=P (¦x-2¦√1 ≥ k/√1) = P(¦x-2¦≥ k)

+1-P(¦x-2¦< k) ∼ 1-[ Φ (k) - Φ (-k)]

=2(1- Φ(k))

Thus we tabulate the probabilities as below

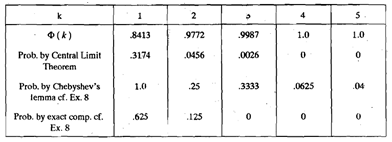
As expected, since the sample size 4 is not large sufficient, the difference between the exact and the approximate probabilities in Example are considerable. Thus the approximation will be better for larger values of n.

Approximations of equations are good for large n but better approximations are acquired by making some corrections, called the continuity corrections, for representing a discrete distribution through a continuous distribution. For the discrete binomial distribution P (x < X < x + 1) is equal to zero if x is an integer hut while this probability is approximated by the normal probability it is never equal to zero. This necessitates the continuity correction. A reasonable approach to get a better approximations to write P (X = x) as equal to

P (x-1/2

P ( x_l ≤ X ≤ x₂ ) as P( x₁-1/2 < X ≤x₂ + 1/2 ). This suggests that a better

approximation to binomial cdf is obtained by using

F(x) ∼ Φ  {(x+1/2 -np)/√(npq))} and

P(x₁≤ X≤ x₂) ∼ Φ  ((x₂+1/2-np)/√(npq)) - Φ ((x₁-1/2 -np)/√(npq))

alternatively of previous equations respectively. In fact, a theoretical justification of why this equation gives a better approximation than previous one can also be given. Thus, we do not go into the theoretical details.