Combined mean

Assume m be the combined mean

Assume x₁ be the mean of first sample

Assume x₂ be the mean of the second sample

Assume n₁ be the size of the 1^st sample

Assume n₂ be the size of the 2^nd sample

Assume s₁ be the standard deviation of the 1^st sample

Assume s₂ be the standard deviation of the 2^nd sample

∴ Combine mean = (n₁x₁ + n₂x₂)/(n₁n₂)

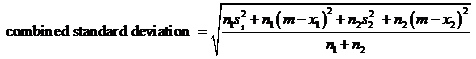
 Illustration

A sample of 40 electric batteries described a mean life span of 600 hours along with a standard deviation of 20 hours.

Other sample of 50 electric batteries described a mean lifespan of 520 hours along with a standard deviation of 30 hours.

If these two samples were combined and utilized in a given project simultaneously, find out the combined new mean for the larger sample and hence find out the combined or pulled standard deviation.

                Size                    x                     s

               40(n₁)              600 hours (x₁)  hours (s₁)

               50 (n₁)             520 hours (x₂)  30 hours (s₂)

Combined mean = (40(600) + 50 (520))/(40 + 50)

=50,000/90

= 555.56

Combined standard deviation