Calculating Variance (σ)
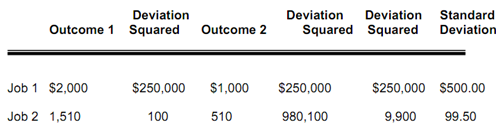
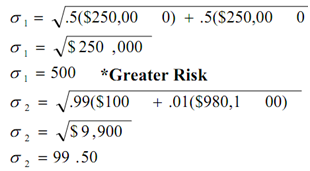
The standard deviations of the 2 jobs are:
The standard deviation is used when there are several outcomes instead of only two.
* An Example
- Job 1 is a job in which income varies from $1000 to $2000 in increments of $100 which are all equally likely.
- Job 2 is a job in which income varies from $1300 to $1700 in increments of $100
that, are all equally likely.
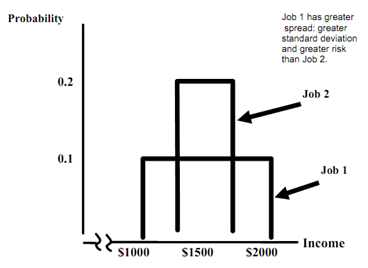
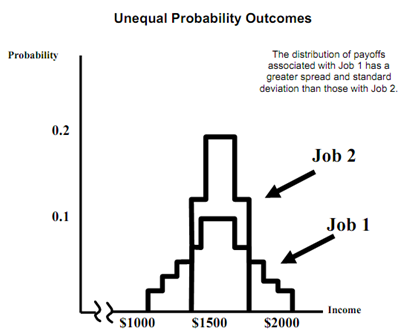
* Outcome Probabilities of Two Jobs
- Job 1: bigger spread and standard deviation
- The peaked distribution: extreme payoffs are much less probable
*? Decision Making
- A risk avoider would select Job 2: same expected income as Job 1 with less risk.
- Assume that we add $100 to each payoff in Job 1 which makes expected payoff = $1600.

The standard deviation is square root of deviation squared.
*? Decision making
- Job 1: the expected income is $1,600 and a standard deviation of $500.
- Job 2: the expected income of $1,500 and a standard deviation of $99.50
- Which job?
- Greater value or less risk?
*? Example
- Suppose a city wants to deter people from wrong parking.
- The alternatives ......
* Assumptions:
1) Wrong parking saves a person $5 in terms of time spent searching for a parking space.
2) The driver is risk neutral.
3) Cost of apprehension is zero.
* A fine of $5.01 would deter the driver from double parking.
- Benefit of wrong parking ($5) is less than the cost ($5.01) equals the average benefit which is less than 0.
* Increasing fine can reduce the cost of enforcement:
- A $50 fine with a .1 probability of being caught results in the expected penalty of $5.
- A $500 fine with a .01 probability of being caught results in the expected penalty of $5.
* The more risk reluctant drivers are, lower the fine is required to be in order to be effective.