Calculate the magnitude of maximum bending moment:

The shear force diagram for the overhanging beam is illustrated in Figure. Draw the loading diagram & bending moment diagram. Determine the magnitude of maximum bending moment & situated the point of contraflexure.

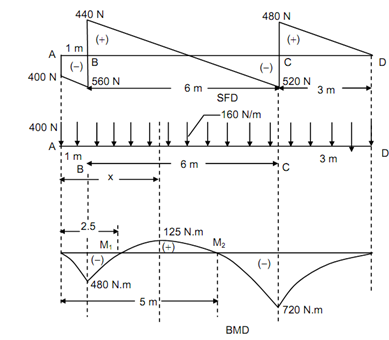
Solution

Let us analyse the shear force diagram specified in Figure .

At A

The shear force diagram suddenly reduces from 0 to - 400 N. It denotes that there is a downward point load of 400 N at point A.

Between A and B

The shear force diagram is an inclined straight line and reduces from - 400 N to - 560 N. It denote that there is a consistently distributed load of (560 - 400 = 160) ⇒ 160 × 1 = 160 kN/m among A and B.

At B

There is a sudden enhances from - 560 N to + 440 N at B. It denotes that there is a support reaction of 1000 N at B.

Between B and C

As the shear force diagram varies linearly from + 440 N to - 520 N among B & C. It denote that a u.d.l. of (440 + 520 = 960) 960 /6= 160 kN/m is acting between B and C.

At C

At C, the shear force diagram enhance suddenly from - 520 kN to 480 N. It denote that there is a support reaction of 1000 N (520 + 480) at C.

Between C and D

The shear force diagram is an inclined straight line which denote that there is a uniform ally distributed load of 480/3 = 160 kN/m from C to D.

Bending Moment

BM at A and D, M_A = M_D = 0.

 BM at B, M _B =- (400 × 1) - (160 × 1 × (½) ) =- 480 N m

BM at C, M _C = - (160 × 3 × (3/2)) =- 720 N m

Maximum Bending Moment

SF at any section XX among B and C,

F_x = +1000 - 400 - 160x

For maximum bending moment, F_x must be equal to zero.

600 - 160x = 0

∴          x = 3.75 m

∴ M _max            = (1000 × 2.75) - (400 × 3.75) - (160 × 3.75 × (3.75/2)

                            = + 125 N m

Maximum positive bending moment take places at a distance of 3.75 m from the end A, where SF changes sign.

Maximum negative bending moment takes place at a support C where SF changes sign.

∴          M_max (negative) = - 720 N m

Points of Contraflexure

Let M₁ and M₂ be the points of contraflexure, where BM is zero. However at any section XX among B and C at a distance x from the end A.

M _x   = 1000 ( x - 1) - 400x - (160 × x × (x/2) )

or         1000x - 1000 - 400x - 80x² = 0

80x² - 600x + 1000 = 0

8x² - 60x + 100 = 0

2x² - 15x + 25 = 0

(2x - 5) (x - 5) = 0

Therefore,        x = 2.5 m  and   5 m.