Calculate the displacement of a particle:
The displacement of a particle is given by the equation,
x = 10 t 3 - 7 t 2 + 6 t + 2
I. Calculate its displacement & velocity at t = 4 seconds.
II. Also computed the distance travelled in 4th second. Distances are measured in centimeters.
Solution
(i) We have x = 10 t 3 - 7 t 2 + 6 t + 2 .
∴ Displacement, at t = 4 seconds, shall be
x4 = 10 × 43 - 7 × 42 + 6 × 4 + 2
= 640 - 112 + 24 + 2
= 554 cm
Velocity = dx / dt = 30 t 2 - 14 t + 6
∴ at t = 4 sec,
v4 = 30 × 42 - 14 × 4 + 6
= 480 - 56 + 6
= 430 cm / sec.
(ii) Distance travelled in 4th second = x4 - x3
we have and x4 = 554 cm [calculated already]
x3 = 10 × 33 - 7 × 32 + 6 × 3 + 2
= 270 - 63 + 18 + 2
= 227 cm
x4 - x3 = 554 - 227
= 327 cm
The equation of non-uniform rectilinear motion can generally be expressed as
x = x0 + v0 t + (½) a t 2 (where a is the acceleration of the particle/body). The displacement time diagram for this can be illustrated in Figure
In this case, if the increment of displacement increases with time, we have accelerated motion, and v = dx/dt as in the previous case. Also we can write, dx = v dt
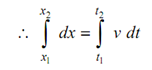
or
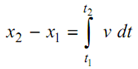
= area under (v - t) diagram between t1 and t2
Figure 5.4
If the velocity of body is not constant and Δv = change in velocity in time Δt, then we may explain acceleration a as the rate of change of velocity.
∴ average acceleration = Δ v / Δ t
and instantaneous acceleration
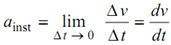
If we consider the equation of motion of a particle given by velocity x = (½) at 2 , then velocity
v = dx /dt= at dt
that means increase in velocity Δv in equal intervals of time Δt is constant during the motion, then the motion is called as motion with constant acceleration.
While in equal intervals of time Δt, increment in velocity Δv1, Δv2 are unequal, after that the motion is called as motion along with variable acceleration.
Also we have
a = dv /dt
∴ dv = a dt
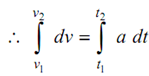
or v2 - v1 = area under acceleration time diagram between t1 and t2.