Assume that the column is a homogeneous circular cylinder with small cross sections loaded by its own weight. The free end of the column will bend away when its height exceeds a certain critical value. Let x=0 be at the top free end and x=L at the base (assume the column is embedded in concrete).

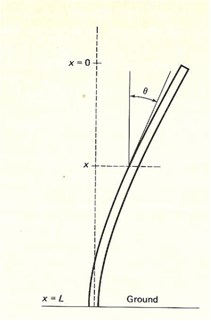
diagram 1:Edwards Penny p.255          

Let θ(x) be the angle between the tangent to the column at the arbitrary point x and the vertical, i.e. the angular deflection of the column.

Question 1.  What other variables and constants do we need to consider? (See the appendix for a derivation of our basic equation (1).  E=Young's modulus, I= moment of inertia of column, ρ is the linear density)

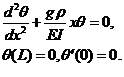
Question 2. Evaluate γ²  E=Young's modulus =2.8x10⁷ lb/in² for a steel column. I=moment of inertia of a circular disk= .25π r⁴. ρ=δA, so g ρ=gδA, A is the cross sectional area. Take gδ=.28 lb/in³. Put this into your answer to question 4 to find the "buckling point" or critical height of a flagpole of diameter 1 in.

Question 3. Transform the differential equation (1) to a Bessel differential equation by first using the substitution z=γ^2/3x  to obtain the differential equation θ''+z θ=0 and then make the substitution  θ(z)=u(t)z^1/2 where t=²/₃z^3/2. Be careful in using the chain rule. You should get the Bessel differential equation : t²u''+tu'+(t²- 1/9)u=0. Show that the solution to our problem in terms of the Bessel function would be the zeros of J_-1/3 (2/3 γx^3/2)

Use Maple (or any other CAS) software to find roots of approximate equation for critical height in Question 2 and to find the zero of the Bessel's function in Question 6. Explain the discrepancy between critical height found in Qiestion2 and Question3.

In Maple use the following commands:

> plot(BesselJ(-1/3,x),x=0..16);

> r1:=RootOf(BesselJ(-1/3,x)=0,x,2);

> h:=solve((2/3)*gam*x^(3/2)=r1,x);