Bidirectional Search:

We've concentrated so far on the searches where the point of view for the search is to find a solution, but not the path to the solution. Like any other searches, we know  and notice the solution, and we know the initial state, but we don't know how to get from one to the other, and the point of view the search is to find a path in the given problem. As in these cases, there in addition to searching forward from the initial state, we can sometimes also search backwards from this kind of problem's solution. This is known as the bidirectional search. 

For example we easily understand, consider the 8-puzzle game in this diagram below, where the main point of the game is just to move the pieces around so by that they are arranged in the right hand diagram. It just that in the search for the solution to this puzzle (the given an arbitrary starting to state); you might start off by moving several of the pieces around to get several of them in their end positions in manner. Then, as you reached closer to the solution state, you might that it work backwards: asking yourself, why and how I can get from the solution to where I am stand at the moment, then reversing the main search path. In this issue yes, you've used a bidirectional search. 

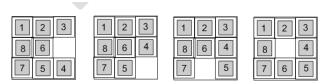
Bidirectional search has the main advantage that search can be done in both directions is only required to go for a depth half that is may be of normal searches, and this can often lead to a drastic cut in the number of paths looked at same like this. For this instance, if we were just looking for a path that is come from one town and goes to another through at most six other towns, we can only have to look for the journey through three towns from both directions, we know that which is fairly easy to do, compare to searching all paths through six towns in a normal way of search. 

Unfortunately, it is just often difficult to apply for a bidirectional search because (a) we don't actually sense the solution, only a description of it (b) there may be too many solutions, and we have to choose a few to work backwards from (c) we can't reverse our operators to work backwards from the solution and (d) we have to record all the paths from both sides to check if any two meet at the same point  - this may take up a lot of memory, and considering through both sets repeatedly could take up more computing time.