Basic indefinite integrals
The first integral which we'll look at is the integral of a power of x.
∫xn dx = (xn +1 / n + 1)+ c, n ≠ -1
The general rule while integrating a power of x we add one onto the exponent & then divide through the new exponent. It is clear that we will have to avoid n = -1 in this formula. If we let n = -1 in this formula we will end up with division by zero. We will make sure of this case in a bit.
Next is one of the simple integrals however always seems to cause problems for people.
∫ k dx = kx + c, c & k are constants
All we're asking is what we differentiated to obtain the integrand it is pretty simple, but it does appear to cause problems on occasion.
Now let's take a look at the trig functions.
∫ sin x dx = - cos x + c ∫ cos x dx = sin x + c
∫ sec2 x dx = tan x + c ∫ sec x tan x dx = sec x + c
∫ csc2 x dx = - cot x + c ∫ csc x cot x dx = - csc x + c
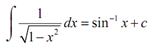
Notice as well that we just integrated two of the six trig functions here. The remaining four integrals are actually integrals which give the remaining four trig functions. Also, be careful with signs here. This is easy to obtain the signs for derivatives & integrals mixed up. Again, we're asking what function we differentiated to obtain the integrand.
Now, let's take care of exponential & logarithm functions.
∫ex dx = ex + c ∫a x dx = ( ax /lna )+ c ( (1/x) dx = ∫x-1 dx = ln |x |+ c
At last, let's take care of the inverse trig & hyperbolic functions.
(1/(x2+1) dx = tan -1 x + c
∫ sinh x dx = cosh x + c ∫ cosh x dx = sinh x +c
∫ sech 2 x dx = tanh x + c ∫ sech x tanh x dx = - sech x + c
∫ csch 2 x dx = - coth x + c ∫ csch x coth x dx = - csch x + c
All we are asking here is what function we differentiated to obtain the integrand the second integral could also be,
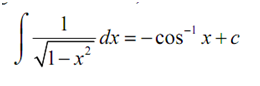
Usually we utilize the first form of this integral.
Now that we've got mostly basic integrals out of the way let's do some indefinite integrals. In all these problems remember that we can always verify our answer by differentiating and ensuring that we get the integrand.