Avoiding Local Minima of multi-layered networks-Artificial intelligence :

The error rate of multi-layered networks over a training set could be calculated as the number of mis-classified instance. However, remembering that there are various output nodes, all of which could potentially misfire (for example, giving a value near to 1 when it would have output 0, and vice- versa), we may be more sophisticated in our error evaluation. In practice the whole network error is calculated as:

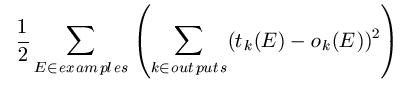
This is not as complexes as it first seem. Simply The calculation involves working out the difference between the observed output for each output unit and the target output and squaring this to make sure it is +ve, then adding all these squared differences for each output unit and for each example.

Back propagation may be seen as utilizing finding a space of network configurations (weights) in order to find a configuration with the least error calculated in the above fashion. The more complexes network structure means that the error surface which is finding may have local minima, and it is a problem for multi-layer networks, and we look at ways around it below.  Even if a learned network is in a local minima, yet it can perform sufficiently, and multi-layer networks have been used to great effect in real world situations (see Tom Mitchell's book for a description of an ANN which can drive a car!)

One way solve the problem of local minima is to use random re-start as discussed in the chapter on search techniques. Different first random weightings for the network  can mean that it converges to different local minima, and the best of these may be taken for the learned ANN. otherwise, as described in Mitchell's book, a "committee" of networks could be learned with the (possibly weighted) average of their decisions taken as an overall decision for a given test example. Another option is to try and skip over some of the smaller local minima, as explained below.

Adding Momentum

Assume a ball rolling down a hill. As it does so, it achieves momentum, so that its speed increases high and it becomes harder to stop. As it rolls down the hill towards the valley floor (the global minimum), it may occasionally wander into local hollows. However, it can be that the momentum it has obtained keeps it rolling up and out of the hollow and back on track to the valley floor.

The crude analogy discussed one heuristic technique for avoiding local minima, called adding momentum, funnily sufficient The method is simple: for each weight remember the previous value of Δ which was added on to the weight in the final epoch. While updating that weight for the current epoch, add on a little of the previous Δ. How little to make the additional extra is controlled by a parameter α called the momentum, which is put to a value between 0 and 1.

To see why this must help bypass local minima, note that if the weight change carries on in the direction it was going in the previous epoch, then the movement shall be a little more pronounced in the current  epoch. This effect will be compounded as the search continues in the similar direction. Finally when the trend reverses, then the search might be at the global minimum, in which case it is chanced that the momentum would not be adequate to take it anywhere other than where it is. On the other hand, the search may be at a fairly narrow local minimum. In this case, even though the back propagation algorithm dictates that Δ will change direction, it might be that the additional extra from the previous epoch (the momentum) can be sufficient to counteract this effect for a few steps. These few steps can be all that is needed to bypass the local minimum.

In addition to getting over some local minima, when the gradient is constant in 1 direction, adding momentum will increase the size of the weight change after each epoch, and the network might converge quicker. Notice that it is possible to have cases where (a) the momentum is not adequate to carry the search out of a local minima or (b) the momentum carries the find out of the global minima into a local minima. This is why this technique is a heuristic method and should be used somewhat carefully (it is used in practice a great deal).