Analytical models

Analytical tools  are very important.  It may  be hard  to check  the  correctness of a machine by trying it in several possible  initial  conditions with  all possible  inputs; sometimes it is more easier  to create a mathematical model  and then solve  a theorem about  the model.

For some  systems, such  as pure  software calculations, or the addition circuitry in a computer, it is possible  to find correctness or speed  with  just a model  of the  system in question.  For other  machines, such  as fuel injectors,  it is not possible to solve the correctness of the controller without also modelling the environment to which  it is inter connected, and then check the behaviour of the coupled system of the environment and controller.

To provide some  of these  tradeoffs, we can do a very simple  analysis of a robot  moving toward a light.  Imagine that we manage it so that the robot's speed at time t, V [t], is related to the difference between the real  light  level,  X[t], and  a given light  level, Xdesired; that is, we may model  our control  method with the difference relation

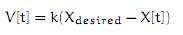
Now, we require to model  the world. For simplicity, we take the light level to the robot's position); in addition we consider the robot's position at time t is its position at time t - 1 plus its speed at time t - 1.

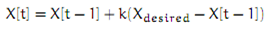
Now,  for a required value  of k, we can calculate how the system will act over time, by resulting the difference relation in X.

These same types of analyses may be given to robot control  machine as well as to the temporal characteristics of voltages in a digital circuit, and even to problems as not related as the  result of a monetary policy  decision  in economics.  It is very important to check that  treating the machine as moving in discrete time stamp  is an approximation to underlying continuous dynamics; it may create models that are simpler to analyze, but it needs sophisticated understanding of sampling to check the effects of this approximation on the answer of the results.