Reference no: EM13837744

Question:

Problem 1:

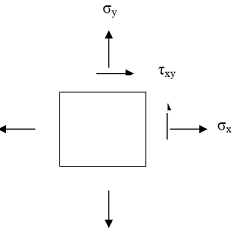
A steel beam with yield strength, σ_yield = 300 MN/m² is under a stress state as follows:

σ_x = 30 MN/m²
σ_y = 150 MN/m²
σ_xy = 45 MN/m²

Using the Mohr's circle method, determine the following:

a) The principal normal stresses and the maximum shear stress

b) Sketch a diagram the orientation of the planes of the principal normal stresses and maximum shear stress relative to the original stress σ_x and σ_y

The normal and shear stresses on a plane 30° counterclockwise from the horizontal plane where the 150 MN/m² stress is acting. Under this stress state, what is the safety factors using the Tresca failure theory, the Rankine failure theory and the Von Mises Theory?

Problem 2:

A steel bar of circular section 160 mm in diameter is to be used as a column with both of its end pin jointed.

a) If the stress limit is 240 MN/m² and the modulus of elasticity of steel is 2x1011 N/m², calculate the safe load if the length of the column is 8 m with a safety factor of 1.75?