Reference no: EM13517701

PROBLEM 

Dr. Konur is the Sherriff of Rolla and right now he needs to assign policemen to the different shifts.

There are 50 policemen he can assign a shift. There are 4 different shifts:
- Shift 1: Starts at 6:00am and ends at 6:00pm
- Shift 2: Starts at noon and ends at midnight
- Shift 3: Starts at 6:00pm and ends at 6:00am
- Shift 4: Starts at midnight and ends at noon
Since different shifts have different start and end times, assigning a policeman to different shifts has different costs. Specifically, a policeman costs $100, $110, $150, and $175 in shifts 1, 2, 3, and 4, respectively. Also, there should be a specific number of policemen available in different time periods to make Rolla safe. The minimum numbers of policemen needed for each time period are given in the table below.

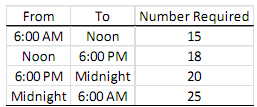
Since Rolla is on a tight budget, Dr. Konur wants to minimize the total cost of the police station he is managing by determining the integer number of policemen to assign to each shift such that at least the minimum number of policemen required in each time period is available for each time period.

a) Mathematically formulate an integer linear programming model for Dr. Konur's problem by defining your decision variables, and expressing your objective and objective function, and constraints using your decision variables. Combine everything to get the final formulation.

b) Answer the following questions independent of each other and without solving the problem and explain your reasoning briefly.

a. If Dr. Konur could assign a fractional number of policemen to any shift, would that increase costs? Yes or No or Maybe? Explain your answer briefly.

b. If Dr. Konur had to assign at least 20 policemen to shift 1, would that increase costs? Yes or No or Maybe? Explain your answer briefly.