Reference no: EM13851905

1. A civil engineering has modelled the deflection behaviour of a cantilever beam using a second-order differential equation. Cantilevers are beams that are fixed at one end and may have a weight suspended from the other end. The weight causes the beam to bend in such a way that the deflection downwards, y, is related to the horizontal distance, x, from the fixed end, according to a differential equation of the form:

where k is determined by the stiffness of the beam and a is the length of the beam. (All distances are in metres.)

a. For a beam that is 1.5 m long, find y in terms of x and k.

b. When x = 1.5, y = 0.031. Find the value of k.

c. The quantity dy/dx gives the inclination of the beam to the horizontal. Find the angle of the beam to the horizontal when x = 0.75 m; that is, approximately at the mid-point of the beam.

2. A civil engineer needs to know the population growth pattern of a town for the purpose of infrastructure planning. He has noted that the rate of growth of the town's population (N) is 5% of its population at any time t years. If its population is currently N0 = 100 000 people (at t = 0), find the following items for using in the infrastructure planning process:

a. the population (Nt) at any time t in terms of initial population (N0) and t

b. the population in 20 years time.

3. A civil engineer is analysing a hemispherical water reservoir of radius "a".

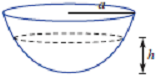
a. Show that the volume of water with a depth of h is given by Πh²/3(3a-h)

A certain hemispherical bowl has a radius of 10 metres.

b. The bowl is being filled with water at a rate of 30 m³ per minute. When the depth is 4 m, find the rate (in m per minute) at which the depth of the water is increasing.

c. Find, using calculus, the approximate change in the volume of the water in the bowl, when the depth of the water in the bowl increases from 4 to 4.01 m.

4. Use Euler's method to obtain an approximation to the value of y (2) using a step size of (i) h = 0.5 (ii) h = 0.1 (iii) 0.01.

dy/dx = y + x/yx

Where, y(1) = 2

Comment on the precision of your result (use a spreadsheet for you calculation and attach the calculation table with your assignment).

5. Two boats, A and B, start at a common point (0, 0) and move with velocity vectors

v_A(t) = ti+ (t² - t) j and v_B(t) = -ti+ (t² + t) j; t ?[0, 4].

Distance is measured in metres and time in seconds.

a. How far apart are they at t = 2?

b. What is the angle between their respective directions at t = 2?

c. At what time, if any, are the acceleration vectors of the two boats perpendicular to each other?

6. Identify the level curves of f(x, y) = √x² + y². Sketch a few of them.

7. Find the partial derivatives ∂f/∂x, ∂f/dy, ∂²f/∂2x, ∂f/∂y², ∂²f/∂y∂x, ∂²f/∂x∂y for the function

f(x,y) = e^xy + xy

8. Find the volume V of the solid bounded by the three coordinate planes and the plane 3x+2y+5z = 6.

9. a. Find the two coupled first order differential equations for the following initial value problem

3x²y"-xy'+y=0; where y(1)=4 and y'(1)=2

b. Sketch a slope field diagram for the differential equation for the stated values of x

dy/dx = -x

x = -3, -2, -1, 0, 1, 2, 3

10. Use three numerical methods and n = 4 for approximating the value of the following integral.

₀∫²e^x2dx