Reference no: EM131266817

Assignment: Modelling and Simulation with MATLAB

Question 1 DC Motor System

Modelling a Brushed DC Motor System

DC motors are widely used in control of marine vehicles (ROVs/AUVs) in maritime industry and in design and control of robots in robotics as well as applications in other industries. Attached datasheet is for several Maxon dc (direct current) motors (permanent magnet dc motors). Select one motor from the datasheet, one tachometer or encoder and gearbox. A motor servo amplifier is used to control the motor and has a gain of K. of which value you should select and its input is in the range of 0 to 10 V.

- Develop mathematical equations for the motor system to relate the input voltage to armature current, shaft speeds (including main shaft's speed and gearbox's speed) and angular displacement/s;

- Write the transfer function 1) between the shaft speed and input voltage, 2) between the shaft angle and the input voltage;

- Write a state space model; and

- Draw a block diagram model.

1.2 MATLAB Programming

Make MATLAB programs to solve the above developed mathematical equations and to plot the following variables vs time: input voltage, armature current, speed/s and shaft angle/s.

Question 2 Ship Manoeurving System

1 Modelling of Ship's Hull Manoeuvring Dynamics

The model scaled vessel named Hoorn is shown in Figure 2. The vessel has twin propellers driven by two separate motors, and a rudder driven by a servo motor. The vessel turns in three ways: 1) by rudder only, 2) by twin propellers only, and 3) by both rudder and twin propellers.

(1) Develop a mathematical model for the ship hull manoeuvring dynamics (turning motion) to relate the ship course (yaw, Iv), yaw rate (r), rudder angle (8) and propeller speeds (n i and n2). The vessel goes forward when the port propeller runs counter-clockwise and the starboard propeller runs clockwise, and the vessel reverses when the port propeller runs clockwise and the starboard propeller runs counter-clockwise.

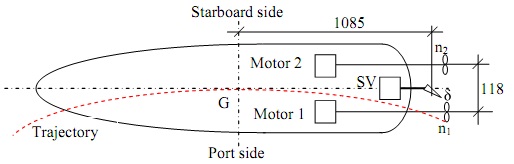
Figure 2 Model scaled vessel Hoorn with twin propellers and rudder (SV = servo motor)

Use the following numerical values:
- Moment of inertia about z-axis (Jr): 22.5 [kgm²];

- Distance from the rudder to G: 1085 [mm];

- Distance between twin propellers: 118 [mm];

- The mass of vessel: 63.4 [kg];

- The maximum speed of propeller: 1000 [RPM];

- The maximum drag force generated by each propeller is assumed to be 50 N;

- The water resistance torque coefficient between the hull and water is K_δ = 6.5 Nm/rad/s;

- The rudder moment constant is K_δ = 2.0 Nm/rad (the rudder turning torque is assumed to be proportional to the rudder angle, i.e. To = K_δδ Nm);

- The equations for trajectory (assume a value of the ship speed) are = usinΨ + vcosΨ
S_t = u cosy/ - v sin NJ (where u is surge velocity [m/s], and v is sway velocity [m/s], x and y are positions in x-axis and y-axis, respectively).

(2) Represent the derived equation's in the following forms:

- Transfer function R(s)/A(s) when the vessel turns by the rudder only;
- Transfer function R(s)/N(s) when the vessel turns by the propellers only, running at the same speeds (8 = 0, n1 = n2 = n);
- A state space model; and
- A block diagram model.

2.2 MATLAB Programming

Make MATLAB program/s to solve the differential equations you developed in 2.1 by
- MATLAB built-in solver;
- A numerical integration method
In your program, write codes to plot the following variables:
- The yaw rate r(t) vs time t;
- The yaw angle w(t) vs time t;
- The trajectory of the vessel.