Reference no: EM13872531
1. Alison is a nurse who happens to be very risk-averse when it comes to financial matters. She makes $45,000 per year and has just inherited $10,000 from her great aunt Sylvia, who died last week of stress-induced heart failure while playing canasta. (Sylvia was 93 when she died.) Alison is trying to decide what to do with the $10,000. After researching rates on the Internet, she narrows her choices down to 2 options:
a. Put the money in a Savings Account with the following expected compound interest rates:
Now 1 Year from Now 2 yrs from NowAfter That
2.5% 3.0% 3.5% 3.5%
b. Put the money in a mutual fund with the following probabilities:
• P(Goes Down 10% over 5 years) = 5%
• P(Stays the same over 5 years) = 25%
• P(Goes up 30% over 5 years)=45%
• P(Goes up 50% over 5 years)=25%
Given Alison's strong risk-aversion, what is her best course of action and what is her risk adjusted expected value? Please use a 5-year planning horizon. You may either solve this problem by hand or use the PrecisionTree software (recommended).
2. You are the head of Human Resources for a 2500-person high-tech Massachusetts company. The company has been plagued recently by a very high (>20%) turnover rate (meaning that 20% of current employees leave the company each year). This is wreaking havoc on the company's stability and profitability, and you have been asked by the company's CEO to make this high turnover stop by modifying hiring practices.
You decide to use logistic regression to try to predict which candidate new employees will stay with the company for at least 5 years. You suspect that the following 5 parameters are important:
• Candidate's age
• Number of years candidate has been married
• Number of children (under age 18) candidate has
• Number of years the candidate attended college
• Average tenure in the candidate's previous 3 jobs, in years
Your assistant has analyzed data from 50 of your past employees and has developed the following table (a Microsoft Excel file is included below):
|
Past Employee
|
Age at Hire
|
No. of Years Married at Hire
|
No. of Kids at Hire
|
No. of Years of College
|
Ave Tenure in previous 3 jobs
|
Stayed >5 years?
|
|
Joe
|
21
|
0
|
0
|
0
|
6
|
Y
|
|
Pete
|
47
|
15
|
2
|
2
|
9
|
Y
|
|
Sara
|
26
|
2
|
3
|
2
|
3
|
N
|
|
Billy-Bob
|
23
|
0
|
0
|
4
|
4
|
N
|
|
Angie
|
32
|
10
|
2
|
0
|
2
|
N
|
|
Occam
|
43
|
0
|
2
|
0
|
4
|
N
|
|
Luigi
|
35
|
15
|
0
|
0
|
6
|
Y
|
|
Candy
|
60
|
20
|
1
|
8
|
15
|
Y
|
|
Joey
|
49
|
0
|
0
|
4
|
8
|
Y
|
|
Mark
|
20
|
0
|
0
|
4
|
5
|
N
|
|
Willis
|
28
|
1
|
2
|
4
|
2
|
N
|
|
Rodolfo
|
27
|
0
|
0
|
8
|
4
|
N
|
|
Cynthia
|
33
|
3
|
4
|
2
|
4
|
Y
|
|
Lew
|
55
|
35
|
6
|
4
|
15
|
N
|
|
Jane
|
47
|
22
|
0
|
2
|
6
|
N
|
|
Allison
|
26
|
4
|
1
|
2
|
5
|
Y
|
|
David
|
29
|
10
|
3
|
4
|
8
|
N
|
|
Riley
|
38
|
16
|
1
|
0
|
10
|
Y
|
|
Herb
|
64
|
40
|
2
|
0
|
13
|
N
|
|
Mikey
|
22
|
4
|
1
|
4
|
5
|
N
|
|
Fred
|
22
|
0
|
0
|
4
|
5
|
Y
|
|
Ellen
|
39
|
11
|
2
|
0
|
3
|
N
|
|
Norton
|
34
|
12
|
2
|
0
|
2
|
Y
|
|
Quince
|
28
|
4
|
0
|
5
|
4
|
N
|
|
Peggy
|
19
|
0
|
0
|
0
|
6
|
Y
|
|
Slatts
|
21
|
0
|
0
|
4
|
1
|
Y
|
|
Jack
|
47
|
0
|
3
|
5
|
8
|
Y
|
|
Patty
|
26
|
2
|
1
|
5
|
10
|
Y
|
|
Kate
|
23
|
0
|
0
|
4
|
11
|
Y
|
|
Alex
|
32
|
12
|
3
|
0
|
6
|
Y
|
|
Katie
|
43
|
21
|
4
|
4
|
6
|
Y
|
|
Matthew
|
35
|
4
|
0
|
4
|
2
|
N
|
|
Kelly
|
60
|
14
|
0
|
8
|
4
|
N
|
|
Norbert
|
49
|
23
|
3
|
4
|
4
|
Y
|
|
Christo
|
20
|
2
|
1
|
4
|
6
|
N
|
|
Eddie
|
28
|
2
|
0
|
0
|
2
|
N
|
|
Beaver
|
27
|
0
|
0
|
0
|
2
|
Y
|
|
Peter
|
33
|
0
|
1
|
5
|
7
|
Y
|
|
Nomar
|
55
|
34
|
5
|
8
|
4
|
N
|
|
Ramon
|
47
|
20
|
2
|
5
|
8
|
N
|
|
Tom
|
26
|
8
|
2
|
8
|
3
|
N
|
|
Tommie
|
29
|
0
|
0
|
4
|
3
|
N
|
|
Thomas
|
38
|
0
|
3
|
4
|
3
|
Y
|
|
Anton
|
64
|
44
|
6
|
4
|
13
|
Y
|
|
Carol
|
22
|
5
|
1
|
0
|
8
|
Y
|
|
Bonnie
|
22
|
0
|
0
|
4
|
10
|
N
|
|
Marty
|
39
|
0
|
2
|
8
|
2
|
N
|
|
Alice
|
34
|
12
|
3
|
4
|
4
|
N
|
|
Jake
|
28
|
1
|
1
|
4
|
5
|
N
|
|
Archie
|
19
|
0
|
0
|
0
|
3
|
N
|
a. Use the Logistic Regression function in Palisade'sStatTools to develop an equation that indicates the probability that a candidate will leave before 5 years and submit that equation (with all terms clearly identified). NOTE: To receive full credit, you must include the final output page from the Logistic Regression analysis of the Palisade StatTools package.
b. Using the equation developed in a) above, predict the probabilities that each of the following candidates will leave before 5 years:
|
Candidate
|
Age
|
No. of Years Married
|
No. of Kids
|
No. of Years of College
|
Ave Tenure in previous 3 jobs
|
|
Sue Ellen
|
23
|
0
|
2
|
0
|
5
|
|
Bobby
|
49
|
23
|
3
|
4
|
6
|
|
J. R.
|
33
|
7
|
4
|
4
|
7
|
3. SMART
a. Andrea is house hunting with her husband. They are both 28 years old, have no children, and have a combined income of $110,000 per year. After looking at over 50 houses, they have narrowed their choices down to 4 located in the towns of Maynard, Stow, Hudson, and Bolton. The parameters that are important to them are commute, price, school system, and availability of good local Chinese food. After much soul-searching and discussion, they are able to construct the following table rating each option on each attribute (10 is best and 0 is worst):
|
|
Maynard
|
Stow
|
Hudson
|
Bolton
|
|
Commute:
|
8
|
7
|
6
|
5
|
|
Price:
|
$275,000
|
$375,000
|
$250,000
|
$425,000
|
|
Schools:
|
5
|
7
|
4
|
7
|
|
Chinese Food:
|
6
|
8
|
7
|
6
|
Use the SMART technique to determine which house Andrea should buy, given the following relative weights: Commute: 5, Price: 20, Schools: 10, Chinese Food: 25
b. Keith is the manager of a food processing company and needs to replace a worn out packaging machine with a new one. He has a limited budget and has narrowed his choices down to three: (i) Aztec, (ii) Barton and (iii) Congress. The criteria that are important to him are depicted by the following hierarchy:
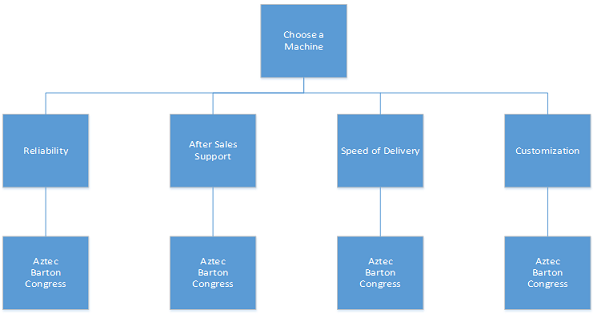
Keith has decided to use AHP to help him make his decision.He has conducted a pairwise comparison of the criteria as represented by the following table:
|
Pairwise Comparison
|
Most Important Criterion
|
How Much More Important?
|
Numerical Ranking
|
|
Reliability- After Sales Support
|
Reliability
|
Somewhat Strongly
|
4
|
|
Reliability-Speed of Delivery
|
Reliability
|
Strongly
|
5
|
|
Reliability-Customization
|
Reliability
|
Somewhat Strongly
|
4
|
|
After Sales Support-Speed of Delivery
|
After Sales Support
|
Weakly
|
3
|
|
After Sales Support-Customization
|
Customization
|
Very Weakly
|
2
|
|
Speed of Delivery-Customization
|
Customization
|
Weakly
|
3
|
Synthesize Keith'srankings and compute the Consistency Ratio (CR). Show your work.
Finally, Keith has pairwise compared each of the alternatives in terms of Reliability, After Sales Support, Speed of Delivery and Customization as shown in the following four matrices.
Reliability
|
|
Aztec
|
Barton
|
Congress
|
|
Aztec
|
1
|
3
|
4
|
|
Barton
|
|
1
|
2
|
|
Congress
|
|
|
1
|
After Sales Support
|
|
Aztec
|
Barton
|
Congress
|
|
Aztec
|
1
|
|
|
|
Barton
|
2
|
1
|
|
|
Congress
|
3
|
4
|
1
|
Speed of Delivery
|
|
Aztec
|
Barton
|
Congress
|
|
Aztec
|
1
|
|
|
|
Barton
|
2
|
1
|
4
|
|
Congress
|
3
|
|
1
|
Customization
|
|
Aztec
|
Barton
|
Congress
|
|
Aztec
|
1
|
5
|
3
|
|
Barton
|
|
1
|
4
|
|
Congress
|
|
|
1
|
Synthesize the alternatives, compute an overall priority ranking for each and declare a winner. Show your work.
4. Six months before its annual convention, the American Medical Association must determine how many rooms to reserve. At this time the AMA can reserve rooms at a cost of $50 per room. The AMA must pay the $50 room cost even if the room is not occupied. The AMA believes the number of doctors attending the convention will be normally distributed with a mean of 5000 and a standard deviation of 1000. If the number of people attending the convention exceeds the number of rooms reserved, extra rooms must be reserved at a cost of $80 per room. Use @RISK simulation to determine the number of rooms that should be reserved to minimize the expected cost to the AMA. Then, for your solution calculate the risk that the AMA will need to obtain 400 or more extra rooms. (Important: You are responsible for showing how you got your results.)