Circles - Theorem
Theorem: If two arcs of a circle or of congruent circles are congruent, then the corresponding chords are equal.
Theorem: (Converse of Theorem): If two chords of a circle or of congruent circles are equal, then corresponding arcs are congruent.
Theorem: The perpendicular from the centre of a circle to a chord bisects the chord.
Theorem: (Converse of Theorem): The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
Theorem: The perpendicular bisectors of two chords of a circle intersect at its centre.
Theorem: There is one and only one circle passing through three non-collinear points.
Remark:
1. An infinite number of circles can be drawn to pass through a single point.
2. An infinite number of circles can be drawn to pass through two given points.
3. A unique circle can be drawn to pass through three given non-collinear points.
4. If three given points are collinear then a single circle cannot pass through three points. For, if there were a circle which passes through three collinear points A, B, C, then perpendicular from the centre of the line will have to bisect AB, BC and AC and thus this perpendicular intersects this line in three points, which is a contradiction.
Theorems:
(1) Equal chords of congruent circles are equidistant from the corresponding centres.
(2) Equal chords of a circle are equidistant from the centre.
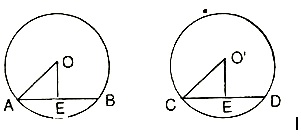
(3) Chords of congruent circles which are equidistant from the corresponding centres are equal.
(4) Chords of a circle which are equidistant from the centre are equal.
Theorems:
(1) If any two chords of a circle the one which is near to the centre is greater.
(2) The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
(3) The degree measure of an arc of a circle is twice the angle subtended by it at any point of the alternate segment of the circle with respect to the arc.
(4) Any two angles in the same segment are equal.
(5) An angle in a semi-circle is a right angle.
(6) The angle subtended in the major segment is acute.
(7) The arc of a circle subtending a right angle at any point of the circle in its alternate segment is a semi-circle.
(8) If a line segment joining two points subtends equal angles at two other points lying on the same side of the line segment, the four points are concyclic i.e., lie on the same circle.
(9) Equal chords of a circle (or of congruent circles) subtend equal angles at the centre (or at the corresponding centres).
(10) If the angles subtended by two chords of a circle (or of congruent circles) at the centre (or at the corresponding centres) are equal, the chords are equal.
Theorems:
(1) The opposite angles of a cyclic quadrilateral are supplementary.
Or
The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
(2) If one side of a syclic quadrilateral be produced, then the exterior angle will be equal to the opposite interior angle.
(3) If the sum of any pair of opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic.
Live Math Experts: Help with Theorem of Circle Assignments - Homework
Expertsmind.com offers help with Theorem of Circle assignment and homework in mathematics subject. Experts mind'smath experts are highly qualified and experienced and they can solve your complex Theorem of Circle math problems within quick time. We offer email based assignment help -homework help service in all math topics including Theorem of Circle .
Math Online Tutoring: Theorem of Circle
We at Expertsmind.com arrange instant online tutoring session in Theorem of Circle math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in Theorem of Circle Math topic and provide you tricky approach to solve complex Theorem of Circle problems.