Geometry Mathematics - Pair of straight lines, Math

Pair of straight lines

1.       (i)      The equation ax² + 2hxy + by2 =0 represents a pair of straight

lines passing through the origin.

(ii)     Let the lines represented by ax² + 2hxy + by² = 0 be y- m₁x = 0 and y - m₂x = 0, then                  

                  

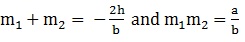
(iii)    If a be the angle between the lines represented by ax² + 2hxy + by² = 0, then

tan q = ±

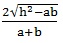
                   Hence,

(a)     If h² - ab > 0 then the lines represented by ax² + 2hxy + by² = 0 will be real and distinct.

(b)     If h² - ab = 0, then the lines are real and coincident.

(c)     If h² < ab, then the lines are imaginary and distinct.

(d)     If a + b = 0, then the lines are perpendicular.

 

2.       The equations of the bisectors of the angles between the lines represented by ax² + 2hxy + by² = 0 is given by

                   

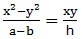
          These bisectors lines will pass through origin also.

 

3.       The equations of the lines passing through the origin and perpendicular to the lines represented by the equation

ax² + 2hxy + by² = 0 is bx² - 2hxy + ay² = 0

 

4.       General equation of second degree in x, y is

ax² + 2hxy + by² + 2gx + 2fx + c = 0

This equation represents two straight lines, if

Δ = abc + 2fgh - af² - bg² - ch² = 0         

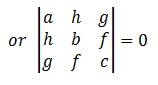
          And point of intersection of these lines is given by         

         

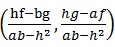
5.       The angle between the two straight lines represented by (i) is given by         

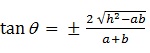
          Hence,

(i)      The lines are perpendicular, if a + b = 0

(ii)     The lines are parallel, if h² = ab

and af² = bg² or

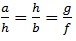
(iii)    The lines are coincident, if g² = ac

 

6.       The equation of the lines parallel to the lines represented by (i) equation and passing through origin is ax² + 2hxy + by² = 0.

 

7.       The equation of the bisectors of the angles between the lines represented by (i) equation is

                  

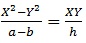
Where X = x - a and Y = g - ß and (a, ß) is point of intersection of the lines. Hence the equation of bisectors will be                   

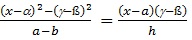
8.       The equation of the lines which joins origin to the point of intersection of the line x + my + n = 0 and curve ax² + 2hxy + by² + 2gx + 2fy + c = 0 can be obtained by making the curve homogeneous with the help of line x + my + n = 0, which is

ax² + 2hxy + by² + 2(gx + fy)                  

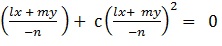
9.       If ax² + 2hxy + by² + 2gX + 2fy + c = 0 represents a pair or parallel straight lines, then the distance between them is given by               

         

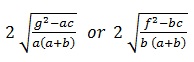
Live Math Experts: Help with pair of straight lines Assignments - Homework

Expertsmind.com offers help with pair of straight lines assignment and homework in mathematics subject. Experts mind’s math experts are highly qualified and experienced and they can solve your complex pair of straight lines math problems within quick time. We offer email based assignment help –homework help service in all math topics including pair of straight lines .

Math Online Tutoring: Pairs of straight lines - Co -Ordinate Geometry

We at Expertsmind.com arrange instant online tutoring session in pair of straight lines math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in pair of straight lines Math topic and provide you tricky approach to solve complex pair of straight lines problems.