Area and volume of solid figure
Solids: Bodies occupying space are called solids. A solid has three dimensions viz., length" breadth and thickness (or depth or height).
Volume: The space occupied by a solid body is called its volume. Volume is measured in cubic units. Its S.I. unit is m3. i.e., the volume of a space region formed by a cube of m.
Cuboid/rectangular parallelopiped:
It is solid with six rectangular faces.
(i) Volume of cuboid = l × b × h
Where: l = length, b = breadth, h = height.
(ii) Surface area of cuboid = 2 (lb + bh + hl)
(iii) Surface area of 4 walls = 2(bh + hl) = 2(l + b) × h
(iv) Surface area of cuboid, in which top face is open
lb + 2 (bh + hl)
(v) Diagonal of faces of cuboid
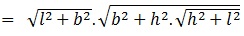
(vi) Diagonal of cuboid =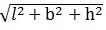 
(vii) Height of cuboid = volume/base area
(viii) Area of base = volume/height
Note:
Volume of material = Ext. volume - Int. volume.
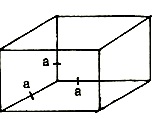
Closed cuboid: If l, b, h are external dimension of closed cuboid of thickness 'a' then internal dimensions are : l - 2a, b-2a, h-2a.
Open cuboid: If the cuboid is an open cuboid then internal dimensions area l- 2a, b - 2a, h - a.
Cube: It is rectangular solid in which every face is square i.e.,
l = b = h = 'a' (say)
(i) Volume of cube = (edge)3 = a3
(ii) Surface area of cube = 2 (aa + aa + aa)
= 2(a2 + a2 + a2)
= 2(3a2) = 6a2 = 6 (edge)2
(iii) Diagonal of face of the cube =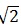 
× a
(iv) Diagonal of cube =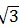 
× a
(v) Edge of cube = (Volume)1/2
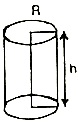
Right circular cylinder: If a rectangle is revolved about its one side as its axis, the solid formed is called a Right circular cylinder.
FORMULAE
(1) Volume of cylinder = (Area of base) × height
= (pr2) × h
= pr2 h m3 or cm3
(2) Curved surface = (Perimeter of base) × height
= (2 × pr) × h
= 2prh m2 or cm2
(3) Total surface area = Area of circular ends + Curved surface area
= 2pr2 + 2prh
= 2pr (r + h) m2 or cm2
where r = radius of the circular base of cylinder
h = height of cylinder.
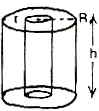
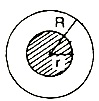
Hollow cylinder: Solids like iron pipes, rubber tubes etc. are in shape of hollow cylinder.
A solid bounded by two co-axial cylinders of the same height, is called a hollow cylinder.
Cylinder with external and Internal radii: Cylinder of height h and with external and internal radii Rand r respectively, we have.
(1) Volume of the material = pR2 h - pr2h
= ph (R2 - r)2
(2) Curved surface = 2pRh + 2prh
= 2ph (R + r)
(3) Total surface area = 2ph (R + r)
+ 2p (R2 - r2)
= 2p (R + r) (h + R - r).
Right circular cone: If a right angled triangle is revolved about one of the sides containing a right angle, the solid thus formed is called a light circular cone.
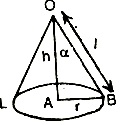
Slant height: Slant height of a right circular cone is the distance of its vertex from any point on the circumference of the base. OL is the slant height of the cone.
Semi vertical angle: It is the angle between the height and the slant height and is usually denoted by a.
(1) Volume of Cone = 1/3 (Area or base) × height
= 1/3 (pier2) × h = 1/3 pier2h cubic units.
(2) Curved Surface Area = pierl sq. units.
(3) Total Surface Area = (pierL + pier2) sq. units.
Frustum of a cone: If a cone is cut by a plane parallel to the base of the cone, then the portion between the plane and base is called the frustum of the cone.
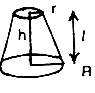
Lateral surface area of frustum of a right circular cone = p
(R + r) sq. units, where R, r be the radii of base and top of the frustum of a cone, h is the height of the frustum and 2 = h2 + (R -r)2.
Volume of a frutrum of a cone =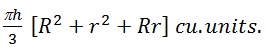 
Total surface area of frustum of right circular cone
= Area of base + Area of top + Lateral surface area
= pR2 + pr2 + p(R + r) = pie [R2 + r2 + l(R + r)] sq. units.
Where l = slant height, r = radius of circular base, h = height.
Where l2 = h2 + r2
Sphere: If a circle is revolved about its diameter, the solid thus formed is called a sphere.
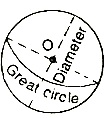
If r = radius of spare
(1) Volume of sphere = 4/3 pier3 cubic units.
(2) Surface area of sphere = 4 piel2
Hemisphere:
(1) Volume of hemisphere =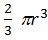 
(2) Curved area: Surface area of hemisphere = 2pr2
(3) Surface (total surface area) of solid hemisphere = 2pr2 + pr2 = 3pr2
A plane through the centre of the sphere cuts it into two equal parts. Each part is called hemisphere.
(4) Spherical shell: Volume of a spherical shell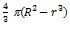 
Prism: A prism is a solid whose side faces are parallelograms and whose bases are equal and parallel rectilinear figures.
A prism is called a right prism, if the axis is perpendicular to the base.
Surface area of a right prism = Perimeter of the base × height sq. units.
Total surface area of a right prism = Lateral area + 2 (area of one box) sq. units.
Volume of right prism = Area of the base × height cu. units.
Pyramid: A polyhedron whose one face is a polygon and the other faces are triangles having a common vertex.
Volume of a right pyramid = 1/2 (area of the base) × height sq. units.
Surface area of a right pyramid = 1/2 (Perimeter of the base × slant height) sq. units.
Total surface area of a right pyramid
= Surface area + area of the base sq.
Live Math Experts: Help with area-and-volume-of-solid-figure Assignments - Homework
Expertsmind.com offers help with area-and-volume-of-solid-figure assignment and homework in mathematics subject. Experts mind’s math experts are highly qualified and experienced and they can solve your complex area-and-volume-of-solid-figure math problems within quick time. We offer email based assignment help –homework help service in all math topics including area-and-volume-of-solid-figure .
Math Online Tutoring: area-and-volume-of-solid-figure
We at Expertsmind.com arrange instant online tutoring session in area-and-volume-of-solid-figure math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in area-and-volume-of-solid-figure Math topic and provide you tricky approach to solve complex area-and-volume-of-solid-figure problems.