Reference no: EM131134404
Exercise: Six Concept Check
Post your 50-word response to the following:
How can you determine if two equations form lines that are perpendicular without graphing?
Give some examples of such equations.
Application Practice
Answer the following questions. Use Equation Editor to write mathematical expressions and equations. First, save this file to your hard drive by selecting Save As from the File menu. Click the white space below each question to maintain proper formatting.
1. Imagine you are at a gas station filling your tank with gas. The function C(g) represents the cost C of filling up the gas tank with g gallons. Given the equation
a. What does the number 2.68 represent?
b. Find C(5).
c. Find C(11).
d. For the average motorist, name one value for g that would be inappropriate for this function's purpose. Explain why you chose that number.
e. If you were to graph C(g), what would be an appropriate domain and range? Explain your reasoning.
2. Examine the rise in gasoline prices from 1997 to 2006. If the price of regular unleaded gasoline in January 1997 was $1.09, and in January 2006, the price of regular unleaded gasoline was $2.03
Use the coordinates (1997, 1.09) and (2006, 2.03) to find the slope, or rate of change, between the two points. Describe how you arrived at your answer.
3. The linear equation
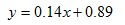
Represents an estimate of the average cost of gas for year x starting in 1993. The year 1994 would be represented by x = 1, for example, because it is the first year in the study. Similarly, 2002 would be year 9, or x = 9.
a. What year would be represented by x = 5?
b. What x-value represents the year 2020?
c. What is the slope, or rate of change, of this equation?
d. What is the y-intercept?
e. What does the y-intercept represent?
f. Assuming this growth trend continues, what will the price of gasoline be in the year 2020? How did you arrive at your answer?
4. The line
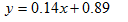
Represents an estimate of the average cost of gasoline each year. The line
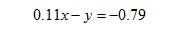
Estimates the price of gasoline in January of each year
a. Do you expect the lines to be intersecting, parallel, or perpendicular? Explain your reasoning.
b. Use the equations of the lines to determine if they are parallel. What did you find?
c. Did your answer to Part b. confirm your expectation in Part a?
|
How do you respond to gene
: Gene Remington, who owns many investments in common stock, says, “I don’t care what a company’s net income is. The stock price tells me everything I need to know!” How do you respond to Gene?
|
|
Ksu corporation has a retained earnings balance
: KSU Corporation has a retained earnings balance of $210,000 on January 1. During the year, a prior period adjustment of $50,000 is recorded because of the understatement of depreciation in the prior period.
|
|
The board of directors is considering either a stock
: The board of directors is considering either a stock split or a stock dividend.They understand that total stockholders' equity will remain the same under either action.
|
|
Probability of expected profits and the variance of profits
: Stringerbelltx: A woman in a highland village in the Andes knits sweaters and sells them for export. She also takes care of her family and helps farm the family land; therefore, the amount of time she can devote to knitting is random. The probability..
|
|
Use equation editor to write mathematical expressions
: To determine if two equations form lines that are perpendicular without graphing, you need to compare the slopes of the two lines. If they are indeed perpendicular, the slope of one line will be the negative reciprocal of the slope of the second line..
|
|
Write an assignment paper on childhood obesity legislation
: Write an Assignment paper on Childhood obesity legislation- What is the health problem being addressed?- What is the underlying biological process of the health problem?
|
|
Create an estimate of your future annual earnings
: Create an estimate of your future annual earnings in a spreadsheet, reporting the following assumptions your actual current retirement savings and average annual salary growth rate.
|
|
What can we infer about the behavior of prices over time
: Will output vary or stay fixed in the long run? Suppose the aggregate demand curve were to remain fixed: What can we infer about the behavior of prices over time?
|
|
What is an output gap in this hypothetical economy
: What is an output gap in this hypothetical economy? Based on your estimate of the output gap, would you expect the unemployment level to be higher or lower than usual?
|