Reference no: EM13325

Problem: Assume that f(x) has the following graph:

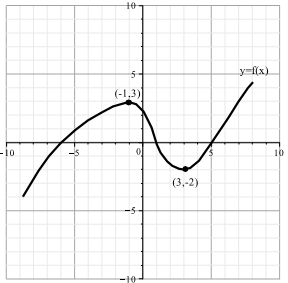
Consider the (1-dimensional) ODE:

x' = f(x):

(a) Find all the xed points, and study their stability.

(b) Draw the phase portrait of the system, as well as the graphs of the solutions in all relevant cases.

(c) Study the bifurcations of the ODE

x' = f(x) + α; α ∈ a parameter:

In particular, determine all the bifurcation values of , and describe the change in behavior before during and after each bifurcation. Make sure to draw the appropriate graphs!

Problem 2 Consider the following matrix:

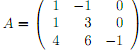
(a) Find a Jordan form of the matrix, as well as a basis that corresponds to that Jordan form.

(b) Compute the exponential matrix eA.

Problem 3 Consider the following linear system of ODE:

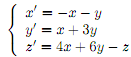
Note that he matrix of this system is exactly the same as in Problem 2.

(a) Study the stability of the xed point (0,0): is it a source (all solutions diverge to 1 from it), sink (all solutions converge to it), saddle (any solution is either convergent to the xed point or diverges to 1), or neither?

(b) Determine stable and unstable subspaces of (0; 0). (The nal answer should be: the stable subspace is spanned by vectors ...., or the stable subspace does not exist.)

(c) Draw a phase portrait of your system in the unstable subspace.

(d) Briefly describe the behavior of solutions to this system. (e.g. "all the solutions except those in xy-plane will go to 1 while rotating around z-axis; the solutions that start in xy-plane will stay in that plane and will rotate on the circle centered at the xed point (0; 0) { 5pts. bonus if you can give me a simple matrix of such a system!)

(e) Write down the general solution of the system above using the initial data

x(0) = x0; y(0) = y0; z(0) = z0:

Problem 4 Consider the following non-linear system

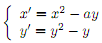
(a) Find the xed points of this system. (depending on a, there may be dierent xed points!)

(b) Study stability of each xed point via linearization. In the case the linearization is inconclusive, use directions of vector-eld analysis (or any other information contained in the equations) to show stability/instability.

(c) Use the information above to determine the bifurcation values for a, and draw the phase portraits for the system before, at, and after each bifurcation. On phase portraits identify the xed points as well as their stable/unstable manifolds (curves) where appropriate.