Reference no: EM131040297
Part -1:
Take the data corresponding to your UIN.
Interest rates are expressed as annualized rates for the term specified. Report your interest rate answers as fractional numbers like 0.11 for 11% per year.
A. Determine the future periodicspot interest rates, at one periodfrom now, on a one-step Ho-Lee model, using current periodic spot interest rate of A1 percent, current spot rate over two periodsof A2 percent, and an annual interest rate volatility of .005 (.5%). Then consider the current spot rate over three periodsof A3 percent to find the future periodicinterest rates in a two-step Ho-Lee model. The period is A4 months. Find the following.
1. The trend (lambda1) ininterest rate in the first period.
2. The trend (lambda2) in interest rate in the second period.
3. The future periodic rate on the upside at the end of one period.
4. The future periodic rate on the downside at the end of one period.
5. The future periodic rate at the up-most branch at the end of two periods.
6. The future periodic rate at the middle branch at the end of two periods.
7. The future periodic rate at the down-most branch at the end of two periods.
8. The future periodic rate at the down-most branch at the end of two periods
B. The cash futures price of a 3-month zero coupon bond with a face value of $100 for delivery in B1 months from now is B2 dollars. Suppose that the current spot interest rate for a term of B3 months is B4 per cent per annum. Assume continuous compounding to answer the following:
9. The forward rate of interest for period B1 months to B1+3 months.
10. The spot rate of interest for period 0 to B1 months.
11. The current fair value of a B1-month zero coupon bond with $100 face.
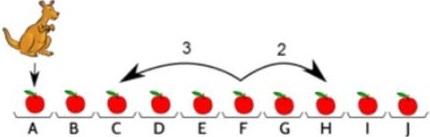
C.Consider C1-month spot interest rates evolving in the following two-step binomial tree over C2 months, i.e., with C1 months in each of the next two steps. The current C2-month spot interest rate is 5.15% and the C3-month spot interest rate is 5.3%. Find the following by assuming monthly compounding.
12. The risk neutral probability for the up move in first step.
13. The risk neutral probability for the up move in second step.
14. The current fair value of a C1-month European call option with a strike price of $974 written on a C2-month zero coupon bond with face value $1000.
15. The current fair value of a C2-month European put option with a strike price of $994 written on a C3-month zero coupon bond with face value $1000.
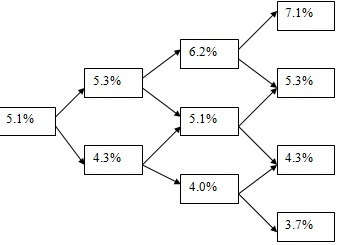
D.Consider D1-month spot interest rates evolving in the following three-step binomial tree over D4 months, i.e., with D1 months in each of the next three steps. The current D3-month spot interest rate is 5.15%, the current D2-month spot interest rate is 5.3%, and the current D4-month spot interest rate is 5.45%. This three-step problem involves calculation of just the third step, because it is an extension of the two-step Problem C. Find the following by assuming monthly compounding.
16. The risk neutral probability for the up move in the last (third) step.
17. The current fair value of a D3-month European call option with a strike price of $974 written on a D4-month zero coupon bond with face value $1000.
18. The current fair value of a D2-month European put option with a strike price of $994 written on a D4-month zero coupon bond with face value $1000.
E. Suppose that you are long in an original portfolio of 20-year bonds with a total face value of E1 million dollars and that you want to hedge the portfolio value against fluctuating interest rates by trading on a 10-year bond and a 30-year bond. You have estimated (given): DV0110 = E2, DV0120 = E3, and DV0130 = E4 per $100 face value of 10-year, 20-year and 30-year bonds, respectively. You have also used yield data on these bonds to estimate the coefficients, b=1.3 and c = 1.6, inthe following regression:
Δyt20 = a + bΔyt10 + cΔyt30 + ε
Using the given data, determine your optimal trading strategy for the 10-year and 30-year bonds to hedge 20-year bonds. Report answers for the following:
19. Face value in dollars of 10 year bonds needed for hedging.
20. Face value in dollars of 30 year bonds needed for hedging.
After hedging, suppose that you observe that the 20-year yield moves by E5 basis points when the 10-year yield moves by 1 basis point and that the 20-year yield moves by E6 basis points when the 30-year yield moves 1 basis point. Then:
21. How much will be your profit or loss corresponding to 30-year yield increasing by 1 basis point?
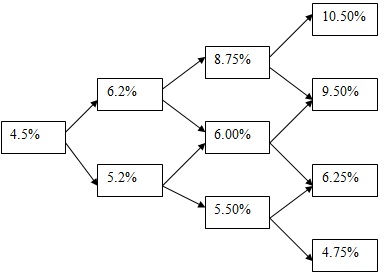
F. A collared floater is like a variable rate bond, but with an upper limit and a lower limit on the rate of coupon payment. Consider, for example, annual rates coupon payment and one-year spot interest rates. In the following table, the current one-year spot interest rate is denoted by rin column (1). Depending on the current spot interest rate, the collared floater with a face value of F1 dollars will pay the holder of this floater a sum a year later, as given in column (2) of the table. The binomial tree below gives the evolution of one-year spot interest rates over a four year period.
22. What is the current fair value of the four-year collared floater if the risk-neutral probabilities in the binomial tree are 0.5 and 0.5 for the up and down moves, respectively?
|
Current Rate, r
(1)
|
Collared Floater with face value F1 pays at the end of the year
(2)
|
|
r< 5%
|
F2
|
|
5% ≤ r ≤ 8%
|
F1 x r%
|
|
r> 8%
|
F3
|
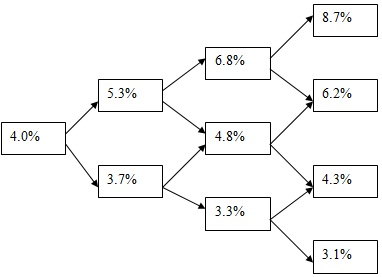
G. A four-year participating cap pays an interest based on a nominal principal of G1, at the end of the year if the current annual spot interest rate, r, is higher than 5%. If the current annual spot rate, r, is less than 5%, the participating cap obligates its holder to lose 30% of (5%-r%) on the nominal principal at the end of the year. The payments are given in column (2) of the following table, given the rates in column (1). The binomial tree below gives the evolution of one-year spot interest rates over a four year period.
23. What is the current fair value of the participating cap if the risk-neutral probabilities in the binomial tree are 0.5 and 0.5 for up and down moves, respectively?
|
Current rate, r
(1)
|
Buyer gets at end of year
(2)
|
|
r > 5%
|
(r% - 5%)xG1
|
|
r ≤ 5%
|
-.30(5% - r%)xG1
|
H. What is the risk premium (spread) of a H1 percent annual coupon, 3.35 year maturity, and 100-face value bond? The bond pays the annual coupon in two equal installmentsand trades now at a quoted spot price of H2. Assume continuous compounding and use the term structure of discount factors for riskless bonds, d(t) = 1 - .03t - .0075t2 + .0015t3. Report answer for the following (Hint: rate at which to discount future cash flows of a risky bond to find the current value is (as per CAPM) the riskless rate which changes with the term of the cash flow plus risk premium which is fixed across all terms; the easier way to solve for risk spread by the method of trial and error, as done an equation solver):
24. Risk Spread (premium) of the bond
Part -2:
Take the data from the attached page corresponding to your UIN.
Interest rates are expressed as annualized rates for the term specified. Report your interest rate answers as fractional numbers like 0.11 for 11% per year.
A. Companies X and Y have been offered the following rates per annum on a 1 million dollars of investments:
Company Fixed Rate Floating Rate
In percent in percent
X A1 LIBOR + 0.5
Y A2 LIBOR + 0.6
Company X requires a fixed rate investment and company Y requires a floating rate investment. Design a swap that will net a bank acting as a financial intermediary (F.I.) 30 percent of the benefits and be equally attractive to both the companies. Draw a complete picture to show the exact transactions and check that the F.I., X, and Y are better off in your swap deal by receiving benefits exactly as asked.Find the following in your swap scheme with all numerical values:
1. Benefit of swap in dollar per year.
2. Return on Y's investment in capital markets in dollar per year
3. Receipt by F.I. from Y in dollar per year.
4. Receipt by X from F.I. in dollar per year
B. The current price of silver is B1 dollars per ounce. The storage costs are B2 dollars per ounce per year, a quarter of which is payable in advance at the beginning of each quarter. Assume that interest rates for all maturities equal B3 percent per annum with continuous compounding. The delivery/maturity of futures contract is B4 quarters.Answer the following:
5. Present value of storage cost in dollars.
6. Current fair value of the futures contract in dollars.
C.This is about the current quoted futures price for a futures contract for delivery in 14 months of a bond paying, semi-annually, coupon at a rate of C1 percent per year on $100 face value, with a maturity of C2 years and 3 months from now. The last coupon payment was 3 months ago. Assume that the term structure is flat with a rate of interest of C3 percent per year. Assume semi-annual compounding for valuation of bond and for determination of conversion factor. Assume continuous compounding for valuation of futures price. Write the answers to the following:
7. Conversion factor.
8. Cash spot price of bond.
9. Cash futures price.
10. Quoted futures price.
D.Find the current fair values of a D1 month European call and a D2 month European put option, using a current stock price of D3, strike price of D4, volatility of D5, interest rate of D6 percent per year, continuously, compounded. Obtain the current fair values of the following:
11. European call by simulation.
12. European put by simulation.
13. European call by Black-Scholes model.
14. European put by Black-Scholes model.
E. Find the implied volatility of a stock when the current market price of the stock is E1 dollars and the current market price of a E2 month European call on the stock, with strike E3 dollars, is E4 dollars. The interest rate is E5 percent per year, continuously, compounded. Assume that Black-Scholes model accurately determines the current market price of the option. Hint: you may need trial and error.
15. Volatility (standard deviation) of the stock implied by the market price of the stock assuming that the market prices European options using Black-Scholes model.
F.Find the values of equity as a call option and default as a put option on assets of a company. The company is formed with F1 of equity capital and F2 of debt borrowed at 10% to be repaid in a year. Assume the liquidation value of assets at the end of the year has four possible outcomes: $7000 with probability .1, $9000 with probability .2, $15000 with probability .4 and $20000 with probability .3. Cost of capital on assets is 15% and cost of capital on equity is 18%. Find the following:
16. Current fair value of assets using basic ideas of finance.
17. Current fair value of equity using ideas of options and basic finance.
18. Current fair value of debt using basic ideas of finance.
19. Cost of capital on debt (express percent as a number) using basic finance ideas.
20. Current fair value of promised debt repayment using cost of debt.
21. Current fair value of default using the idea of options.
G: A G1-month Americancall and put options on futures on an index of stocks with a strike price of G2 dollars for both the options. The current index value is G3 dollars, the risk-free rate of interest is 7 percent per annum, continuously compounded, and the index's volatility is G4 per annum. The index yields a dividend of $3 at 4.5 months (the ex-dividend date) from now. Use a five-step binomial model to calculate the current fair call and put option prices and report your answers as follows:
22. Current fair call option price.
23. Current fair put option price.
H. Use Black's approximation to find the current fair values of a 13-month American call option with a strike price of H1 on a dividend paying stock trading at a current market price of H2, interest rate of H3 percent per year, continuously compounded and volatility of H4 (as a number, not percent). The stock will go ex-dividend every 3 months starting from time zero and the amount of each quarterly dividend is 4 percent of the current stock price. Obtain the following fair values of options needed to find Black's approximate American call value:
24. European call option with maturity at first ex-dividend date.
25. European call option with maturity at second ex-dividend date.
26. European call option with maturity at third ex-dividend date.
27. European call option with maturity at fourth ex-dividend date.
28. European call option with maturity 13 months.
29. Current fair value of American call using Black's approximation
I. You have a Delta-neutral portfolio of options and underlying stocks with Gamma I1 and Vega I2. You can trade two options. The first option has Delta, Gamma and Vega, respectively, of .5, .6 and 1.5. The second option has Delta, Gamma and Vega, respectively, of .4, .7 and 2.5. Determine your hedging strategy to make your portfolio neutral for Delta, Gamma and Vega.
30. How many numbers of the first option will you trade?
31. How many units of the second option will you trade?