Reference no: EM131222413
Problem 1. Consider the payoff matrix shown at right. Suppose agent 1 must move first, and agent 2 can see B agent 1's move before agent 2 chooses a move. Draw the game tree, find all pure-strategy Nash equilibria, C and tell which of them are subgame-perfect.
Problem 2. Below is a 3-player extensive-form game. At each terminal node, the numbers are the utility values for players 1, 2, and 3. At each nonterminal node, the number tells which player will move.
(a) Find the subgame-perfect equilibrium. At every nonterminal node, do two things: circle the move that the player will make, and write the expected utility values for all three players.
(b) Suppose that players 2 and 3 play a minimax strategy profile against player 1, and player 1 plays his/her best response to their strategy profile. At every nonterminal node, do two things: circle the move that the player will make, and write the expected utility values for all three players.
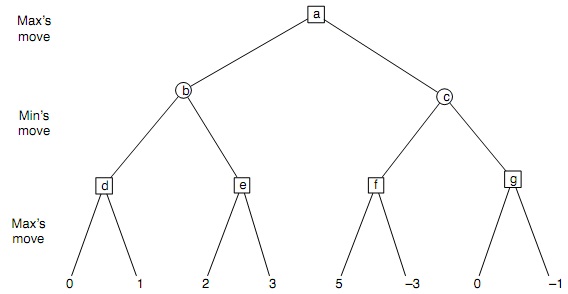
Problem 3. Above is a game tree for a perfect-information zero-sum game. Run the alpha-beta algorithm (by hand) on this game tree. Next to each node, write all of the node's intermediate and final values for α, β, and v.
|
What are various ways in which the textbook proposes
: What are various ways in which the textbook proposes that our understanding of the corporation to its stakeholders can be revised? What are some of the benefits and drawbacks to each proposal?
|
|
Financial statements of the company
: What impact does the grant of these options have on the financial statements of the company? Explain Answer please.
|
|
Determining the chances for the applicant to get a job
: Your script should repeatedly ask the user for a GPA value and compute the student's chances of being hired. It should continue asking for GPA values until a negative number is entered.
|
|
What is the current market price of bonds
: Jackson Corporation's bonds have 19 years remaining to maturity. Interest is paid annually, the bonds have a $1,000 par value, and the coupon interest rate is 9.5%. The bonds have a yield to maturity of 12%. What is the current market price of the..
|
|
Find all pure-strategy nash equilibria
: Consider the payoff matrix shown at right. Suppose agent 1 must move first, and agent 2 can see B agent 1's move before agent 2 chooses a move. Draw the game tree, find all pure-strategy Nash equilibria, C and tell which of them are subgame-perfec..
|
|
President of goodman snack foods company
: Les Moore retired as president of Goodman Snack Foods Company but is currently on a consulting contract for $35,000 per year for the next 10 years.
|
|
Identify the four components of brand position
: Identify current challenges and opportunities for the brand. Explain in 90- to 175- words what strategies you propose for the brand based on the identified challenges and opportunities.
|
|
Write and test the code for the function mysteryfunction
: Write and test the code for the function mysteryFunction that consumes a vector, V, and produces a new vector, W, of the same length where each element of W is the sum of the corresponding element in V and the previous element of V. Consider the p..
|
|
Invest a single amoun
: You invest a single amount of $10,000 for 5 years at 10 percent. At the end of 5 years you take the proceeds and invest them for 12 years at 15 percent. How much will you have after 17 years?
|