Reference no: EM131008881
A proportional controller is to be used to control the pump output pressure in the system shown below
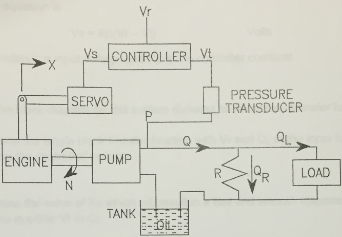
The steady state output torque of the engine is given by the equation
Tss = 1500 X - 25 N fit-lbf
where X is the throttle position in inches and N is the engine speed in rpm. The total combined rotational moment of inertia (I) of the engine and pump combined is 150 ft¬lbf-s2. The output of the pump is related to the engine speed by the equation
Q = 0.1 N gal/min
where N is in rpm. The torque required to drive the pump is determined by the pressure output from the pump
T = 0.5 P ft-lbf
Where P is in psi. The bypass circuit has a constant resistance R of 300 psi/(gal/min).
The voltage output of the pressure transducer is given by the equation
Vt = 0.0001 P Volts
Where P is in psi. The throttle servo is a first order system with a time constant of 1 second and a steady state responsegiven by the equation below.
Xss = 0.5 Vs inches
Where Vs is the voltage input to the servo.
The controller equation is
Vs = Kp(Vr Vt) Volts
where Vr is a reference input voltage and Kp is the controller constant
1. Draw the block diagram for this system showing all necessary transfer functions
2. Determine the single block transfer function with Vr and QL in the input function and P as the controlled variable.
3. Determine the value of Kp which will result in a fast and smooth response to changes in either Vr or QL.
4. Determine the equation for the steady state value of P for given values of Vr and QL using your value of Kp.
5. The system is operating at steady atate with Vr equal to 2 volts and QL equal to 0. QL suddenly changes to 25 gal/min and remains fixed at that value. Plot X, P, and N against time during the transition to a new steady state. These plots may be determined from an exact solution of the differential equation or a numerical solution based in the system equations. A listing of the program with comments explaining the solution must be included with the solution.
|
Standard error of the mean increase
: a) What is the standard error of the mean increase in sales tax revenue collected? b) What happens to the accuracy of the estimate when the interval is constructed using the smaller sample size? c) Find and interpret a 95% confidence interva..
|
|
Causal analysis on global crisis
: For this assignment you will write a 1,500 word Causal Analysis on one of the following: A global crisis (terrorism, pollution, poverty, disease)
|
|
Problem regarding the confidence interval estimate
: How would the 95% confidence interval be worse for the planners? How could they achieve a confidence interval estimate that would better serve their planning needs?
|
|
Find the x-coordinate of the local maximum
: Find the x-coordinate of the local maximum of f(x)=x3-1.2x2-1.8x. Find the x-coordinate of the inflection point of f(x)=x3-2.3x2-1.4x.
|
|
Determine the single block transfer function with vr and ql
: Draw the block diagram for this system showing all necessary transfer functions. Determine the single block transfer function with Vr and QL in the input function and P as the controlled variable.
|
|
Number of foreclosures of family homes
: There were a large number of foreclosures of family homes. In one large community, realtors randomly sampled 36 bids from potential buyers to determine the average loss in home value. The sample showed the average loss was $11,560 with a standard ..
|
|
What is meant by the term myocardial infarction
: What is meant by the term "myocardial infarction" and how does it apply to this scenario? What were the predisposing factors in Mr. E's lifestyle that placed him in the high risk category
|
|
Estimating the costs of lunch in cafeteria
: Meal costs. A company is interested in estimating the costs of lunch in their cafeteria. After surveying employees, the staff calculated that a 95% confidence interval for the mean amount of money spent for lunch over a period of six months is ($7..
|
|
Find dimensions of right circular cylinder of surface area
: Find the dimensions of the right circular cylinder of a minimum surface area (including the circular ends) with a volume of 32π in3.
|