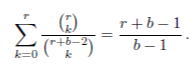Reference no: EM131984968

Part A -

(a) Parasites infest a plant. Suppose that parasites arrive from elsewhere at rate λ > 0 and also individually give birth at rate λ and individually die at rate μ > 0. Explain how to use the theory of detailed balance for continuous-time Markov chains to model this and to establish conditions for existence of statistical equilibrium, and compute the probability of no parasites being on the plant at a specific time when the system is in statistical equilibrium.

(b) Now suppose that it is required to take account of competition between parasites by supposing that the individual death rate is μX when the population size is X. How does your answer change?

Part B -

Let X be a random walk on R with step-distribution defined as follows: if X_n = u then X_n+1 has the shifted "double-headed exponential density" f_u/2(x) = f(x - u/2) = (1/2) exp (-|x - u/2|).

(a) Show that X is l-irreducible, where l(·) is Lebesgue (length) measure.

(b) Show that any set C of the form C = {x : |x| ≤ c}, c >0, is a small set of lag 1.

(c) Let Λ(x) = 1 + x². Using this function; establish that X is geometrically ergodic.

Part C -

A shuffled pack of cards contains b black and r red cards. The pack is placed face dawn on a table, and cards are turned over one at a time. Let B_n denote the number of black cards left just before the n^th card is turned over. (So, for example, B₁ = b.)

(a) Show that M_n = B_n/(r + b - (n-1)), the proportion of black cards left just before the n^th card is revealed, defines a martingale.

(b) Let T be the time at which the first black card is turned over. Compute the probability mass function of this random variable.

(c) Use part (b) and the Optional stopping theorem applied to M_T+1 to show that