Reference no: EM131463317
The design work involves producing layouts for circuit in Fig. 1. Such layouts correspond to the patterns developed on the masks, for use in the fabrication process, as discussed in lectures. Each of the layouts MUST be drawn on a graph paper with stipulated scale (e.g. 1pm per cm). The four masks that need to be defined are: device area, gate stripe, contacts and metal pattern. Produce individual layouts for each device i.e. A, B, C and RL, and also the overall layout for the circuit, in terms of the minimum feature size. Make sure to include the alignment errors between the layouts and minimise the area used.
Description: The circuit in Fig. 1 consists of a two-stage inverter, where the output from the 1st inverter Vo' is fed into the input gate of the 2nd inverter. The driver of both inverters consists of enhancement type n-MOS transistors A and B. Note these transistors have identical aspect ratios. It can be assumed that the threshold voltage VT to be 0.3 V. For the loads, the 1st inverter has an (active) saturated n-MOS transistor C, whilst the 2nd inverter has an (passive) implanted resistor load RL. Note the resistance value of C is equal to the resistance RL, and similarly, the resistance of A is identical to the resistance of B, when the transistors are on.
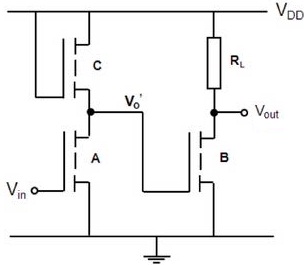
For your design, calculate the dimension of the channel width W for the drivers and respective dimensions of W and L for C and RL. To assist you with the calculation, you can select appropriate value for the output voltage Vo, which corresponds to the logic 0 condition, assuming a logic 1 input to be equal to VDD = 5 V. Note the value of Vo needs to be lower than VT of the driver B in order to ensure that the transistor remains off at logic 0. The value depends on the ratio of the resistances between the driver and load for each inverter. Also for the implanted resistor RL, you can assume a sheet resistance of 150Ω/square, where each square is defined by minimum feature size.
Note for the layouts you must take account the alignment accuracy λa, which can also be assumed to be equal to the minimum feature size. For your calculation, you can assume the following values for the parameters:
i. Minimum feature size λm = 0.5 μm
ii. Supply voltage VDD = 5V (Logic 1 input)
iii. Threshold voltage VT = 0.3 V
iv. Sheet resistance 150 Ω/square
v. Device constant is given as,
β = (μCo)W/L = (βo)W/L where βo = 1.8 x10-4 AV-2
Useful hints:
1. If driver A is on and Vo,' is small then the current through A can be approximated as,
ID = βA[(Vin - VT)Vo' - Vo'2] ≈ βA[Vin - VT)]
With the aid of this current expression and Ohms law, the value of the resistances for driver A and load C can be determined. The aspect ratio of the load C can be obtained using the saturation current (note this load always operates in saturation regime) as,
ID = βc/2(VDD - VT)2.
2. The resistance values for the two loads are the same i.e. Rc = RL. To determine their dimensions i.e. L and W, of the implanted resistor RL. use the given the sheet resistance and consequently calculate the number of squares required. For C, determine the value of W and L accordingly. Note this W/L is not the same as W/L for A or B.
For the Report: Give a brief description of the circuit operation in Figure 1. Include all your calculations and reasons for the assumptions made. Represent all respective individual and overall design layouts in scaled graph paper, in terms of minimum feature size. Use different shading to indicate the different regions and include the alignment errors between respective layouts.