Reference no: EM13251
Question: The two DOF system below has two moving masses M1, M2 with an input force of f(t) applied to M . The characteristics of the system are as follows:
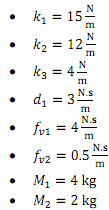
Note: the friction forces fv1 and fv2 can be thought of as damping forces.
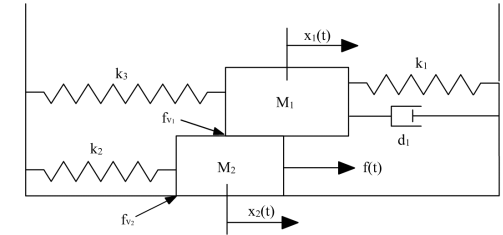
a) Derive the system's dynamics (the governing differential equations) using the Lagrangian method
b) For an output of x1(t) and a state vector of x =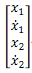 
find the A, B, C and D matrices
Question: Consider the transfer function:
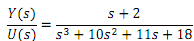
a) Find the differential equation describing the system
b) Write the state and output equation's in Observer Canonical (Left Companion)
c) Draw the block diagram of the system (using the form from part b above); how many states are observable?
Question: In the case of an inverted pendulum shown below, the equations of motion for control are a function of the movement in the horizontal direction and the angular motion of the bob. The angle of the bob is assumed to be sufficiently low to provide a linear model of the system.
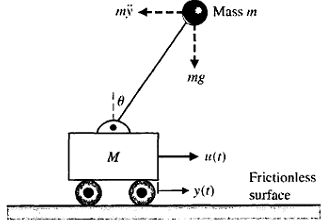
The properties of the system are as follows:
• M- Mass of Cart (5 kg)
• m- Mass (the bob) at end of rod (0.1 kg)
• θ- angular displacement of rod from vertical
• y- displacement in horizontal direction
• l- length of rod (0.5 m)
The sum of the forces in the horizontal direction can be shown to be:
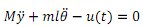(1)
By approximating the pendulum as a point mass, the sum of the moments about the pivot point is:
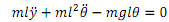(2)
By rearranging equations (1) and (2) and simplifying by assuming M >> m then the state and input matrices are:
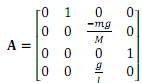
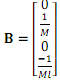
With a state vector given by:
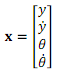
a) What is the rank of the A matrix and what does this tell you about the states used in the state space model? Relate this to the dynamic equations
b) For an output of θ the minimal realisation of the system will have a 2x2 A matrix. For this minimal realisation find the A, B, C, D matrices and the state vector
c) Find the eigenvalues of the system from the state-space model derived in b)
d) Sketch the poles of the system on the complex plane
e) Is the system stable?
f) Using the state space model from b) find the transfer function
|
Retention policy and litigation hold notices
: The purpose of this project is to provide you with an opportunity to create a document retention policy. You will also learn how to serve a litigation hold notice for an educational institute.
|
|
Write the code required to analyse and display the data
: Calculate and store the average for each row and column. Determine and store the values for the Average Map.
|
|
What will be the effects of an increase in the money supply
: What will be the effects of an increase in the money supply
|
|
Discuss the different environmental companies
: Discuss the different agencies, institutes, centers, different environmental companies that are active in UAE.
|
|
Automatic control
: DOF system and Find the differential equation describing the system
|
|
Long-run perfectly competitive equilibrium for the firm
: Evaluate Government intervene and correct this situation?(a) Explain the concept of a concentration ratio. A rise in the price of magarine Explain the impact of external costs and external benefits on resource allocation long-run perfectly c..
|
|
Prepare a marketing plan
: A marketing plan is an essential tool for any marketer, providing direction for a brand, product or organization. A marketing plan describes the marketing environment, marketing objectives and marketing strategies.
|
|
Hrm and ob
: In today's corporate and globalized business environment, HRM (Human Resource Management) is one of the essential tools for the business organizations that determine overall success of the corporation (Amos, Ristow, Pearse & Ristow, 2009).
|
|
Create a simple warm-up program using your g3d
: Create a simple warm-up program using your G3D programming and graphics environment.
|