Toughness

While the load acts upon the specimen or test piece, specific work is done. This work it saved in the specimen or test piece as its strain energy. Whether load P acts upon the specimen or test piece and causes specific displacement, d_L the work finished,

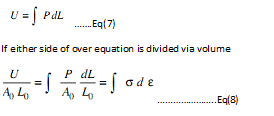
The integral ∫σdε is nothing excepting the area beneath stress-strain curve. It sense that the work done on the specimen or test piece  per unit volume in stretching that is stored in the specimen or test piece  as strain energy, such be measured by region beneath the curve. The maximum elastic energy per unit volume such material can absorb with no attaining plastic state is termed as "resilience's modulus", whilst the energy saved in the test piece or specimen at any stress inside elastic limit might be referred to like resilience.

The toughness of a material is known to be its capability to absorb energy throughout entire plastic and elastic deformation. Region beneath entire stress-strain curve the "toughness's modulus" is measured and is the energy absorbed via material of the specimen or test piece per unit volume upto fracture.

From following figure it can be consider that toughness's modulus will depend on both the eventual tensile strength and strain at fracture and material that is extremely ductile will exhibit a superior toughness's modulus as is the case along with mild steel. Otherwise, modulus of resilience depends on elastic limit or yield strength or proportional limit and so a material along with higher yield strength will contain higher resilience or modulus. Higher toughness is an advantageous property in materials employed for gears, hooks, chains, freight car coupling. Higher resilience is needed in springs.

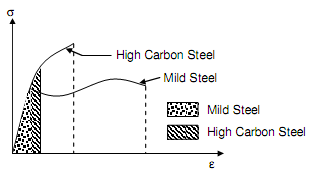
         Figure: σ - ε Curves for High Toughness as Mild Steel and Low Toughness as High Carbon Steel Materials

For ductile materials as mild steel the toughness's modulus may be computed by approximate formula as:

                                Modulus of toughness σ_u ε_f =  ((σ_Y   + σ_u )/2) ε_f..............................Eq(9)

Here σ_Y and σ_u  are correspondingly yield and eventual tensile strengths, and ε_f is the strain like fracture.

Reliance's Modulus is the area of triangle whose height is σ_Y and support is the strain consequent to σ_Y,that is ε_Y. Thus modulus of resilience is ½  σ ε.

Because

e_y = σ_Y/E

                                             Modulus of resilience = σ² /2E...................Eq(10)

Conversely a ductile material is stronger against tension than against shearing stresses. In a tension test piece or specimen, the maximum shearing stress reacts on a plane that is inclined at an angle 45^o along with the axis as represented in above figure (c). Though, due to neck's formation the state of stress modifies considerably. Now until the final fracture of a ductile material represents a characteristics cup-and-cone fracture surface. The cone and cup match at an angle 45^o along with the axis, showing such the last fracture has arisen along these planes all around the periphery. Whether a highly polished test piece or specimen is tested in tension after that on the surface at yield point fine lines will view. These lines are usually inclined beginning of sliding of atomic planes beneath the effect of maximum shearing stress as in above figure (c).