Transconductance Small Signal Model:

Back in the very straining of the transistor era, an engineer at Jim Early, Bell Labs, predicted that there would be a slope to the I_C curves, and that they would all of the project back to the same intersection point on the horizontal axis. Having built that prediction, J_im went down into the laboratory, made the measurement, and confirmed his prediction, therefore showing that the theory of transistor behaviour was being correctly understood. The point of intersection of the V_CE axis is known as the Early Voltage. As the symbol V_E, for the emitter voltage was already taken, they ought to label the Early Voltage V_A instead. (Even though the intersection points are on the negative half of the V_CE axis, V_A is universally quoted as a positive number.)

Generally, the slope is much less than we have illustrated here, and so for any given value of I_C, we can just take the slope of the line as I_C/V_A, and therefore the resistance, which is usually called r₀ is just V_A/Ic. Therefore, we add r₀ to the small signal model for the bipolar transistor. This is illustrated in Figure (a). In a good quality modern transistor, the Early Voltage, V_A shall be on the order of 150-250 Volts. So if we let V_A = 200 V, and we suppose that we have our transistor biased at 1 mA, then r0 =200 V/1 mA = 200 k?, which is usually much larger than most of the other resistors you shall encounter in a typical circuit. In most instances, r₀ can be ignored with no problem.

(b)

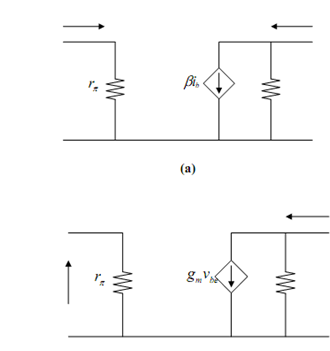
Figure: (a) Including r0 in the Small Signal Model; and (b) Transconductance Small Signal Model

Sometimes this is advantageous to use a mutual transconductance model of Figure (b) rather than a current gain model for the transistor. If we say the input small signal voltage is v, then obviously

i  = v_BE / r_π  =   v_BE / (β/ 40I_C)

But

i  = βi_b  = β v_be  / (β /40Ic) =40Ic v_{be =} g_mv_be

where g_m is called the mutual transconductance of the transistor. Notice down that β has totally cancelled out in the expression for g_m and that g_m based only upon the bias current, I_C, passing through the collector and not on any of the physical properties of the transistor itself.