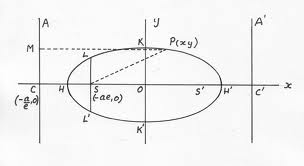
Ellipse:

The ellipse is a curve generated via a point moving such like at any position the sum of its distances from two fix points or called foci is a constant and is equal to the major diameter.

Ellipse Construction by Foci Method

Sketch the major axis AB and minor axis CD and locate the foci F₁ and F₂ via striking arcs centered at C and contain a radius OA equal to one half of the major diameter.

Find out the number of points needed along the circumference of all quadrant of the ellipse for a relatively accurate layout and mark off this number of division points P, Q, R and S among O and F1 on the major axis. It may be desirable to use additional points spaced closer together near F1 in order to form accurately the sharp curvature at the ending of the ellipse. Along with F1 and F2 as centers and the distance AP and BP as radii correspondingly, strike intersecting arcs to locate P on the circumference of the ellipse. Space AQ and BQ are radii for locating points Q. Locate R′ and S′ in a same manner and complete the ellipse by joining P′, Q′, R′, S′ and A by smooth curve or using a French curve.