Coefficient of Coupling:

While two coils are coupled magnetically, it is significant to know how much of the flux generated by one coil is linking with the other. Coefficient of coupling gives an idea about that.

Let us consider again the magnetically coupled coils of Figure Following Eq. (9), inductance of coil1 and coil 2 may be written as :

L₁ = N₁  (φ₁ /i₁ )

L ₂= N₂   (φ₂  /i₂ )

Let Φ₁ be the total flux produced by current i₁ in coil 1 and Φ₁₂ be the part of Φ₁ that is linked with coil 2.

Let                                             φ₁₂ = k₁ φ₁

From Eq. (20),

M = N (φ₁₂ /i₁₂ )= N k₁ φ₁  /i₁ 

Likewise, let Φ₂ be the total flux produced by current i₂ in coil 2 and Φ₂₁ be the part of Φ₂ that is linked with coil1.

Let                       φ₂₁  = k₂ φ₂

From Eq. (2.21),

M = N (φ₂₁ /i₁₂ ) = N₁( k₂ φ₂/ i₁₂)

Multiplying Eqs. (24) and (25), we get,

M ²  = k₁ k₂ N₁ N₂ φ₁ φ₂ / i₁i₂= k₁ k₂  =(  N1 φ1 / i₁₂)( N2 φ2 / i₁₂ )= k₁ k₂  L₁ L₂

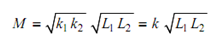
where ∴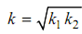

So, From Eq. (26), we obtain,

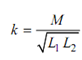
Constant k is called as coefficient of coupling and this is defined as the ratio of mutual inductance M to the square root of the product of inductances of coil 1 and coil 2.

If k =1, you know that the flux because of one coil is fully connected with the other. If k = 0, the flux in one coil does not link with the other coil at all.