Ohm's law for ac circuits:

Ohm's Law for a direct current circuit is a simple relationship among 3 variables: voltage (E), current (I), and resistance (R). The formulas becomes

I= E/R  

E =IR

R = E/I

In alternating current circuits containing negligible or zero reactance, the same formulas apply, as long as you are sure that you use effective current and voltage.

Effective amplitudes

The effective value for an alternating current sine wave is the root mean square, or RMS, value. The RMS current or voltage is 0.707 times the peak amplitude. On the other hand, the peak value is 1.414 times the RMS value.

If you are told that an alternating current voltage is 35 V, or that an alternating current is 570 mA, it is generally understood that this refers to a sine wave RMS level, unless otherwise.

Purely resistive impedances

When the impedance in an alternating current circuit is so that the reactance X has a negligible effect, and that practically all of current and voltage exists through and across a resistance R, Ohm's Law for an alternating current circuit can be expressed as

I = E/Z

E = IZ

Z = E/I

where Z is necessarly equal to R, and the values I and E are RMS current and voltage.

Complex impedances

When determining relationship among current, voltage and resistance in an alternating current circuit with resistance and reactance which are both significant, things get interesting.

The formula for absolute value impedance in the series RLC circuit,

Z² = R² + X²

so Z is equal to square root of R² +X². This is the length of vector R + jX in complex impedance plane. This formula applies for series RLC circuits.

The absolute value impedance for the parallel RLC circuit, in which resistance is R and reactance is X, can be defined by formula:

Z² = (RX)²/(R²+ X²) Therefore, Z is equal to RX divided by square root of R² +X².

Problem:

A series RX circuit has R = 50.0 Ω of resistance and X=-50.0 Ω of reactance, and 100 V_ac can be applied. What is the current?

 
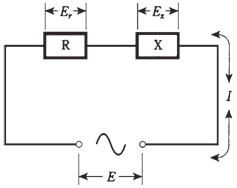
Figure--  A series RX circuit. 

First, calculate Z² = R² +X² = 50.0² +(-50.0)² = 2500 + 2500 = 5000; Z is square root of 5000, or 70.7 Ω. Then I = E/Z = 100/70.7=1.41 A.