Differentials and Derivatives:

One of the most general encountered applications of the mathematics of dynamic systems involves the relationship among position and time for a moving object.  Below figure represents an object moving in a straight line from position P₁ to position P₂.  The distance to P₁ from a fixed reference point, point 0, along with the line of travel is represented through S₁; the distance to P₂ from point 0 by S₂.

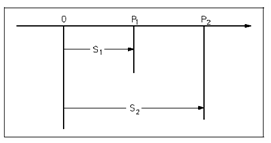
Figure: Motions Between Two Points

If the time recorded by a clock, while the object is at position P₁  is t₁, and if the time when the object is at position P₂  is t₂, then the average velocity of the object among points P₁  and P₂ equals the distance traveled, divided by the elapsed time.

V_av = S₂ - S₁/t₂ -t_{1                                         . . .}(1)

If positions P₁ and P₂ are close together, the distance traveled and the elapsed time is little. The symbol Δ, the Greek letter delta, is used to indicate changes in quantities.  Therefore, the average velocity while positions P₁ and P₂ are close together is often written using deltas.

V_av = ΔS/Δt = S₂ - S₁/t₂ -t_{1                       . . .}(2)

While the average velocity is frequent an significant quantity, in several cases it is essential to know the velocity at a given instant of time.  This velocity, called the instantaneous velocity, is not the similar as the average velocity, unless the velocity is not changing along with time.