Zero-Bias Equilibrium
In a p-n junction, with no an external applied voltage, an equilibrium condition is arrived at in which a potential variation is formed across the junction. This potential difference is termed as built-in potential Vbi.
Later than joining p-type and n-type semiconductors, electrons that are near the p-n interface tend to diffuse into the p region. As electrons diffuse, they depart positively charged ions (donors) in the n region. Likewise, holes near the p-n interface start to diffuse into the n-type region leaving fixed ions (acceptors) along with negative charge. The regions near the p-n interfaces lose their neutrality and become charged, creating the space charge region or depletion layer.
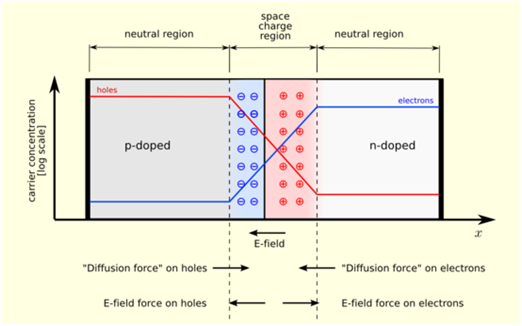
Figure: A p-n junction in thermal equilibrium with zero bias voltage applied. Electrons and holes concentration are reported correspondingly with blue and red colored lines. Gray regions are charge neutral. Light red zone is charged positively. Light blue zone is charged negatively. The electric field is displayed on the bottom, the electrostatic force on electrons and holes and the direction in which the diffusion tends to move electrons and holes.
The electric field that is created by the space charge region opposes the diffusion procedure for both electrons and holes. There are 2 concurrent phenomena: the diffusion process which tends to produce more space charge and the electric field produced by the space charge which tends to counteract the diffusaion. The carrier concentration profile at equilibrium is displayed in figure with blue and red colored lines. As well shown are the two counterbalancing phenomena which establish equilibrium.
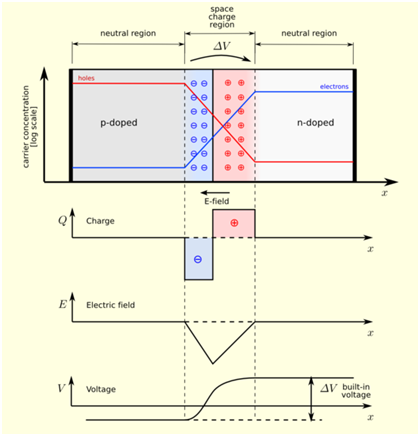
Figure: A p-n junction in thermal equilibrium with zero bias voltage applied. Within the junction, plots for the charge density, the electric field and the voltage are reported.
The space charge region is a zone with a net charge that is provided by the fixed ions (donors or acceptors) which have been left uncovered via majority carrier diffusion. While equilibrium is arrived at, the charge density is approximated through the displayed step function. Actually, the region is totally depleted of majority carriers (leaving a charge density equal to the net doping level), and the edge among the space charge region and the neutral region is quite sharp. The space charge region has similar charge on both sides of the p-n interfaces, so it extends farther on the less doped side.