Write down the system of differential equations for mass system and the spring above.

Solution

To assist us out let's first take a rapid look at a situation wherein both of the masses have been moved.  It is demonstrated below.

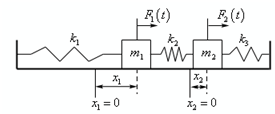
Before proceeding let's see that it is only a representation of a classic case, but most definitely not each possible case.

Under this case we're assuming as both x₁  and x₂  are positive and that x₂ - x₁ < 0 , or conversely, both masses have been moved to the right of their regards equilibrium points and that m₁ has been moved farther than m₂ .Therefore, under these assumption on x₁  and x₂  we know that the spring on the left along with spring constant k₁ has been stretched past it's natural length whereas the middle spring that have constant k₂ and the right spring that have constant k₃ are both in compression.

Also, we've demonstrated the external forces, F₁ (t) and F₂ (t), as present and acting into the positive direction. They do not, in practice, require to be present in every situation where in case we will suppose that F₁ (t) = 0 and/or F₂ (t) = 0. Similarly, if the forces are actually acting in the negative direction we will after that suppose that F₁ (t) < 0 and/or F₂ (t) < 0.

Before starting we need to discuss a little bit about how the middle spring will act as the masses move. Now there are all the possibilities which we can have and the influence each will have on x₂- x₁.  Note that under each case the amount of stretch/compression in the spring is specified by x₂ - x₁ even though we won't be using the absolute value bars while we set up the differential equations.

1.      If both mass move similar amount in similar direction then the middle spring will not contain changed length and we'll contain x₂ - x₁ = 0.

2. If both masses move in the positive direction afterwards the sign of x₂ - x₁ will tell us which has moved more. If m₁ moves more than m₂ then the spring will be in compression and x₂ - x₁ > 0 . Similarly, if m₂ moves more than m₁ then the spring will have been stretched and x₂ - x₁ < 0 .

 3. If both masses move into the negative direction we'll contain pretty much the opposite behavior like #2.  If m1 shifts more than m₂ then the spring will have been stretched and x₂ - x₁ > 0 .  Likewise, if m₂ shifts more than m₁ then the spring will be in compression and x₂ - x₁ < 0.

 4. If m1 moves in the positive direction and m₂ moves in the negative direction then the spring will be in compression and x₂ - x₁ < 0 .

 5. Finally, if m₁ moves in the negative direction and m₂ moves in the positive direction then the spring will have been stretched and x₂ - x₁ > 0 .

 Here, we'll use the figure above to assist us develop the differential equations and then ensure that they will also hold for the other cases suitably.

Let's start off through getting the differential equation for the forces acting upon m₁. Now there is a rapid sketch of the forces acting on m₁ for the figure as given above.

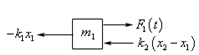
Under this case x₁ > 0 and therefore the first spring has been stretched and therefore will exert a negative that is to the left force upon the mass. The force from the primary spring is then -k₁ x₁ and the "-" is required since the force is negative but both k₁ and x₁ are positive.

Subsequently, as we're assuming that m₁ has moved more than m₂ and both have moved in the positive direction we also identify that x₂ - x₁ < 0.  Since m₁ has moved more than m₂  we identify that the second spring will be in compression and thus the force must be acting in the negative direction on m₁ and hence the force will be k₂ (x₂ - x₁).  Note that since k₂ is positive and x₂ - x₁ is negative such force will have the accurate sign that is negative.

Then the differential equation for m₁ is,

m₁ x₁′′= - k₁ x₁ + k₂ (x₂ - x₁ ) +F₁ (t)

Remember that it will also hold for all the other cases. If m₁ has been moved in the negative direction the force form the spring on the right that acts on the mass will be positive and -k₁ x₁ will be a positive quantity for this case. After that, if the middle is has been stretched that is x₂ - x₁ > 0 then the force from this spring on m₁ will be in the positive direction and k₂(x₂ - x₁) will be a positive quantity for this case. Thus, this differential equation contains for all cases not just the one we exemplified at the start of this problem.

Let's here we write down the differential equation for all the forces which are acting on m₂ .  Now there is a sketch of the forces acting upon this mass for the situation sketched out in the figure as given above.

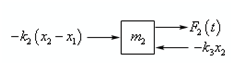
For this case  x₂  is positive and therefore the spring on the right is in compression and will exert a negative force upon m₂ and therefore this force must be -k₃ x₂ , here the "-" is needed since both k₃  and  x₂  are positive. Also, the middle spring is until now under compression but the force which it exerts on this mass is this time a positive force, not like in the case of m₁ , and therefore is given through -k₂ (x₂ - x₁). The "-" on that force is needed since x₂ - x₁ is negative and the force must be positive.

Then the differential equation for m₂ is,

m₂ x₂′′ = - k₃ x₂ - k₂(x₂ - x₁) + F₂ (t)

We'll leave this to you to verify that that differential equation does actually hold for all the other cases.

Placing all of this together and doing a little rewriting will after that give the follow system of differential equations for this situation.

m₁ x₁′′ = - (k₁ + k₂) x₁ + k₂ x₂ + F₁(t)

m₂ x₂′′ = k₂ x₁ - (k₂ + k₃) x₂ + F₂(t)

it is a system to two linear second order differential equations which may or may not be non-homogeneous depending if there are any external forces, F1 (t) and F2 (t) , acting upon the masses.