The Null Hypothesis - H0:  γ₁ = γ_{2 = ...  =}  0  i.e.  there is no heteroscedasticity in the model

The Alternative Hypothesis - H1:  at least one of the γ_i's are not equal to zero i.e. the squared residuals are related to one of the independent variables.

Reject H0 if nR²   >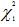  

Regression Analysis: sqresi versus totexp, age, ...

* sqnk is highly correlated with other X variables

* sqnk has been removed from the equation.

The regression equation is

sqresi = 0.00086 - 0.000117 totexp + 0.000765 age + 0.00007 nk

         + 0.000000 sqtotexp - 0.000009 sqage + 0.000000 totexpage

         + 0.000026 totexpnk - 0.000077 agenk

Predictor         Coef     SE Coef      T      P     VIF

Constant      0.000857    0.007288   0.12  0.906

totexp     -0.00011676  0.00004906  -2.38  0.017  49.148

age          0.0007649   0.0003256   2.35  0.019  73.466

nk            0.000072    0.002941   0.02  0.980  24.250

sqtotexp    0.00000019  0.00000010   2.00  0.045  13.958

sqage      -0.00000879  0.00000394  -2.23  0.026  62.515

totexpage   0.00000021  0.00000097   0.21  0.831  37.830

totexpnk    0.00002598  0.00001464   1.77  0.076  18.920

agenk      -0.00007694  0.00007905  -0.97  0.331  32.566

S = 0.0112807   R-Sq = 1.2%   R-Sq(adj) = 0.6%

Analysis of Variance

Source            DF         SS         MS     F      P

Regression         8  0.0022313  0.0002789  2.19  0.026

Residual Error  1493  0.1899897  0.0001273

  Lack of Fit    639  0.0804237  0.0001259  0.98  0.601

  Pure Error     854  0.1095659  0.0001283

Total           1501  0.1922209

 332 rows with no replicates

Source     DF     Seq SS

totexp      1  0.0006642

age         1  0.0000000

nk          1  0.0000026

sqtotexp    1  0.0005240

sqage       1  0.0005895

totexpage   1  0.0000013

totexpnk    1  0.0003292

agenk       1  0.0001206

MTB > let k4=1502*0.012

MTB > print k4

Data Display

K4    18.0240

Inverse Cumulative Distribution Function

Chi-Square with 8 DF

P( X <= x )        x

       0.95  15.5073

Since nrsq = (1502*0.012) 18.024 > 15.5073 = 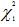, there is sufficient evidence to reject H0 which suggests that there is heteroscedasticity in the model from White's general heteroscedasticity test at the 5% significance level.  Both Breusch Pagan test and White's general heteroscedasticity test seem to indicate that totexp is the culprit as the T value is significant and the P-value is 0.000.