Vogel's Approximation Method (VAM)

This method is a heuristic and usually provides a better starting solution than the two methods described above. However, VAM generally yields an optimum, or close to optimum, starting solution.

The steps of the process are as shown below:

Step 1: 

Evaluate a penalty for each row (column) by subtracting the smallest cost element in the row (column) from the next smallest cost element in the same row (column).

Step 2:

Identify the row or column with the largest penalty, breaking ties arbitrarily. Assign as much as possible to the variable with the least cost in the chosen row or column. Regulate the demand and supply and cross-out the satisfied row or column. When a row and a column are fulfilled concurrently, only one of them is crossed out and the enduring row (column) is allocated a zero supply (demand). Row or column with zero demand or supply should not be used in computing future penalties—(in Step 3)

Step 3:

(a) When exactly one row or one column stays uncrossed out, stop.
(b) When only one row (column) with positive supply (demand) stays uncrossed out, determine the fundamental variables in the row (column) by the least-cost technique.
(c) If all uncrossed-out rows and columns have (assigned) zero supply and demand, determine the zero basic variables the least-cost method.  Stop.
(d) Or else, re-computed the penalties for the uncrossed-out rows and columns then go to step 2.
(e) Notice that the rows and columns with assigned zero supply and demand should not be used in computing these penalties.

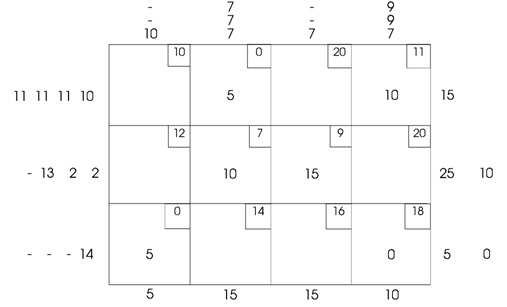
The cost of the program is Shs 315 which happens to be optimal. The given version of VAM breaks ties between penalties arbitrarily.  However, breaking of ties may be crucial in rendering a good starting solution.