VARIATION OF PARAMETERS - HIGHER ORDER DIFFERENTIAL EQUATIONS

We now require taking a look at the second method of finding a particular solution to a differential equation. Since we did while we first saw Variation of Parameters we'll go through the complete process and derive up a set of formulas which can be used to generate an exact solution.

Though as we saw earlier when looking at 2^nd order differential equations this method can lead to integrals which are not easy to calculate. Therefore, while this method can always be used, not like Undetermined Coefficients, to at least write down a formula for an exact solution this is not always going to be possible to actually find a solution.

Therefore let's get started on the process. We'll begin this with the differential equation,

y⁽ⁿ⁾ + p_n-1(t) y^(n-1) + ......+ p₁(t) y' + p₀(t) y = g(t)            (1)

And suppose that we've got a fundamental set of solutions, y₁(t), y₂(t),  ..., y_n(t), as for the associated homogeneous differential equation.

Since we have a fundamental set of solutions to the homogeneous differential equation we this time know that the complementary solution is,

y (t ) = c1 y1 (t ) + c2 y2 (t ) + L + cn yn (t )

The method of variation of parameters includes trying to get a set of new functions, u₁(t), u₂(t),  ..., u_n(t), hence,

Y(t) = u₁(t)  y₁(t) + u₂(t)  y₂(t) +    .............     + u_n(t)  y_n(t)     (2)

It will be a solution to the non-homogeneous differential equation. So as to determine if it is possible, and to get the u_i(t) if this is possible, we'll require a total of n equations including the unknown functions which we can hopefully solve.

All of the equations are easy. The guess, (2), will require satisfying the original differential equation, (1). Therefore, let's start taking several derivatives and since we did when we first looked at variation of parameters we'll create some assumptions along the way which will simplify our work and into the process create the remaining equations we'll require.

So, the first derivative of (2) is,

Y(t) = u₁ y'₁ + u₂ y'₂+    .............     + u_n y'_n + u'₁ y₁ + u'₂ y₂ + .....+ u'_n y_n  

Remember that we rearranged the results of the differentiation process some now and we dropped the (t) part on the u and y to create it a little easier to read. Here, if we remain differentiating it this will quickly turn into unwieldy and therefore let's make as assumption to simplify things now. Since we are after the u_i(t) we must probably try to ignore letting the derivatives on these turn into too large.  Therefore, let's make the assumption as,

 u'₁ y₁ + u'₂ y₂ + .....+ u'_n y_n = 0

The natural question at that point is does this still make sense to do? The response is, if we end up along with a system of n equations which we can solve for the u_i(t) so yes this does make sense to do.

Obviously, the other answer is, we wouldn't be creating this assumption if we didn't know that this was going to work. Though, to accept this answer needs that you trust us to make the exact assumptions therefore maybe the first answer is the best at such point.

The first derivative of (2) at this point is,

Y'(t) = u₁ y'₁ + u₂ y'₂+    .............     + u_n y'_n  

And therefore we can now take the second derivative to find,

Y''(t) = u₁ y''₁ + u₂ y''₂+    .............     + u_n y''_n + u'₁ y'₁ + u'₂ y'₂ + .....+ u'_n y'_n  

It looks an awful lot like the original first derivative earlier to us simplifying this thus let's again make a simplification. We'll again need to maintain the derivatives on the u_i(t) to a minimum therefore this time let's suppose that,

u'₁ y'₁ + u'₂ y'₂ + .....+ u'_n y'_n = 0

And with this assumption the second derivative turns into,

Y''(t) = u₁ y''₁ + u₂ y''₂+    .............     + u_n y''_n

Expectantly you're starting to notice a pattern develop now. If we carry on this process for the first n -1 derivatives we will get there at the following formula for such derivatives.

Y^(k)(t) = u₁(t)  y₁^(k) + u₂ y₂^(k) +    .............     + u_n y_n^(k)

k = 1,2,....,n-1                                      (3)

To find to each of these formulas we also had to suppose that,

u'₁(t)  y₁^(k) + u'₂ y₂^(k) +    .............     + u'_n y_n^(k) = 0,                    k = 0,1,.....n-2              (4)

And recall that the 0^th derivative of a function is simply the function itself. Therefore, for illustration,

y⁽⁰⁾₂ =  y₂(t).

Remember as well that the set of assumptions in (4) really provides us n -1 equations in terms of the derivatives of the unknown functions as: u₁(t), u₂(t),  ..., u_n(t),.

All we require to do then is finish generating the first equation we started that process to find (that is plugging (2) in (1)). To perform this we'll require one more derivative of the guess. Differentiating the (n -1)^st derivative, that we can get from (3), to find the n^th derivative provides,

Y⁽ⁿ⁾(t) = u₁(t)  y₁⁽ⁿ⁾ + u₂ y₂⁽ⁿ⁾ +    .............     + u_n y_n⁽ⁿ⁾ + u'₁ y₁^(n-1)+ u'₂ y₂^(n-1) +    ...  +u'_n y_n^(n-1)

Now we will also not be making any assumptions to simplify that but in its place just plug that along with the derivatives specified in (3) in the differential equation, (1)

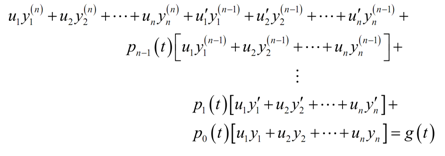
Subsequently, rearrange this a little to fins,

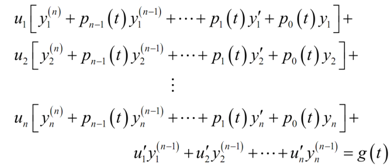
Recall that y₁(t), y₂(t),.., y_n(t) are all solutions to the homogeneous differential equation and therefore all the quantities in the [ ] are zero and that reduces down to,

u'₁ y₁^(n-1)+ u'₂ y₂^(n-1) +    ...  +u'_n y_n^(n-1) = g(t)

Therefore this equation, with those specified in (4), gives us the n equations which we required.  Let's list them all out now for the sake of completeness.

u'₁ y₁+ u'₂ y₂ +    ...  +u'_n y_n = 0

u'₁ y'₁+ u'₂ y'₂ +    ...  +u'_n y'_n = 0

u'₁ y''₁+ u'₂ y''₂ +    ...  +u'_n y''_n = 0

.

.

.

u'₁ y₁^(n-2)+ u'₂ y₂^(n-2) +    ...  +u'_n y_n^(n-2) = 0

u'₁ y₁^(n-1)+ u'₂ y₂^(n-1) +    ...  +u'_n y_n^(n-1) = g(t)

Therefore, we have got n equations, but see that just like we found when we did this for 2^nd order differential equations the unknowns in the system are not u₁(t), u₂(t),..., u_n(t) but instead they are the derivatives, u₁′(t), u₂′ (t),..., u_n′ (t). It isn't a major problem though.  Given we can solve this system we can after that just integrate the solutions to find the functions that we are after.

Also, recall that the y₁(t), y₂(t),..., y_n(t) are assumed to be identified functions and therefore they along with their derivatives (that appear into the system) are all identified quantities in the system.

This time, we require thinking about how to solve such system. If there aren't various equations we can just solve this directly if we need to. Though, for large n (and this won't take much to find large here) that could be fairly tedious and prone to error and this won't work at all for general n like we have here.

The most excellent solution method to use at this point is here Cramer's Rule. We have used Cramer's Rule some time in this course; although the best reference for our purposes now is when we used this while we first defined Fundamental Sets of Solutions back into the 2^nd order material.

By using Cramer's Rule to solve the system the resulting solution for all u_i′ will be a quotient of two determinants of nxn matrices. The denominator of all solutions will be the determinant of the matrix of the known coefficients,

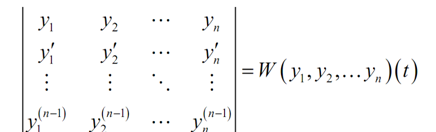
This though, is just the Wronskian of y₁(t), y₂(t),..., y_n(t) as noted above and since we have assumed that such form a fundamental set of solutions we also identify that the Wronskian will not be zero. It in turn tells us that the system above is actually solvable and all of the assumptions we apparently made out of the blue above did actually work.

The numerators of the solution for u_i′ will be the determinant of the matrix of coefficients along with the i^th column swapped along with the column n(0, 0, 0,...., 0, g (t)). For illustration the numerator for the first one, u₁′ is,

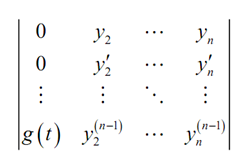
Here, by a nice property of determinants in case we factor something out of one of the columns of a matrix so the determinant of the resulting matrix will be the factor times the determinant of new matrix. Conversely, if we factor g (t) out of this matrix we get there at,

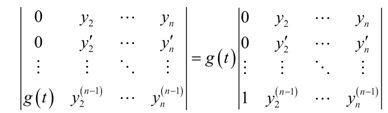
We did that only for the first one, although we could just as easily done that with any of the n solutions.

Thus, let W_i represent the determinant we find by replacing the i^th column of the Wronskian along with the column (0,0,0,...,0,1) and the solution to the system can so be written as,

u'₁ = (g(t) W₁(t))/(W(t)), u'₂ = (g(t) W₂(t))/(W(t)),........., u'_n = (g(t) W_n(t))/(W(t))

Wow! It was a lot of effort to make and solve the system but we are almost here. With the solution to the system on hand we can now integrate all of these terms to find out just what the unknown functions, u₁(t), u2(t),..., un(t) we've finally along are.

u'₁ = ∫((g(t) W₁(t))/(W(t))), u'₂ = ∫((g(t) W₂(t))/(W(t))),........., u'_n = ∫((g(t) W_n(t))/(W(t)))

At last, a particular solution to (1) is then specified by,

Y(t)= y₁(t)∫((g(t) W₁(t))/(W(t))) + y₂(t) u'₂ = ∫((g(t) W₂(t))/(W(t)))+.........+ y_n(t)∫((g(t) W_n(t))/(W(t)))

We must also note that in the derivation process now we supposed that the coefficient of the y(n) term was particular and which has been factored in the formula above. If the coefficient of above term is not one so we will require making sure and dividing it out before trying to use this formula.

Before we work an illustration here we actually should note that whereas we can write this formula down in fact computing these integrals may be all but not possible to do.