Steps for solving the problems when more than two coplanar forces are acting on the rigid body:

The steps are as;

1. Check the Problem for the concurrent or Non concurrent

2. Count the Total Number of forces acting on body.

3. First resolved all the forces in vertical and horizontal direction.

4. Make direction of force away from the body.

5. Take upward forces as positive, down ward force as negative, Left hand force as negative, and the Right hand force as positive.

6. Take sum of all horizontal parts that is ∑ H

7. Take sum of all vertical parts that is, ∑V

8. Find out the resultant of the force system using,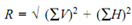 

9. Find angle of resultant by using tan   =    ∑V/ ∑H

10. Take care of signs of          ∑V and ∑H.