The Equilibrium Consumption Combination equilibrium for the person occurs at the point where the indifference curve, shown by II, is tangent to the budget line, portrayed by BB. This sets the marginal rate of substitution of consumption for leisure equal to the wage rate. Suppose the former was higher than the latter, as shown by the indicated by the star. By working one unit less the individual will give up w units of consumptions. His marginal rate of substitution is bigger than this number, implying that the person would be willing to give up more than w units of consumption to gain an extra unit of leisure. Hence, the individual should work less. By moving to the point indicated by the circle he would increase his utility. A point on a higher indifference curve would not be feasible. It would lie outside of the budget line. Therefore, is too expensive for the person. A point on a lower indifference curve would imply a lower level of utility.
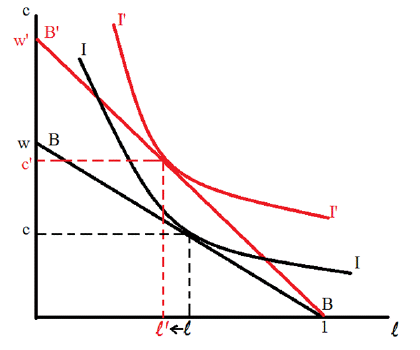
1.1.4. The Impact of a Change in Wages. What happens when the wage rate, w, changes? Specifically, assume that it rises from w to w0. The situation is shown in Figure 2. The rise in the wage rate causes the budget constraint to rotate outward from BB to B0B. The persons equilibrium moves to the new point (l0; c0). In the situation portrayed, consumption rises while leisure falls. The impact of a wage increase on leisure is ambiguous in general, however.
To see this, the above move is broken down into two steps, as shown in Figure. Let the person labor at the new wage, w0, but reduce his endowment of time so that the new budget line passes through his old consumption/leisure point (l; c). In particular, you need to take away (w0 - w)(1 - l) in income or (w0 - w)(1 - l)=w0 in time. This leads to a parallel downward shift in the budget constraint from B0B0 to B00B00 that goes through the point (l; c). This is called a compensated shift in income. To prove that it goes through the point (l; c) note following the (negative) compensation the persons budget constraint is given by
c0 + w0l0 = w0 - (w0 - w)(1 - l):
It will be shown that the consumption point (l; c) satis.es this equation.
To see this, set c0 = c and l0 = l; that is, can the individual still buy