The Null Hypothesis - H0:  There is no heteroscedasticity i.e. β₁ = 0

The Alternative Hypothesis - H1:  There is heteroscedasticity i.e. β₁ 0

Reject H0 if Q = ESS/2 >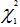

MTB > let k2=sum(c20)/1519

MTB > let c22 = c20/k2

C20 = sqres

C22 = gt

Regression Analysis: gt versus income, totexp, age, nk

The regression equation is

gt = 1.15 + 0.000130 income - 0.00135 totexp + 0.00095 age - 0.0424 nk

Predictor       Coef    SE Coef      T      P

Constant      1.1494     0.2336   4.92  0.000

income     0.0001296  0.0007340   0.18  0.860

totexp     -0.001345   0.001034  -1.30  0.193

age         0.000948   0.005248   0.18  0.857

nk          -0.04239    0.08131  -0.52  0.602

S = 1.54236   R-Sq = 0.1%   R-Sq(adj) = 0.0%

Analysis of Variance

Source              DF        SS           MS       F        P

Regression         4     5.364        1.341  0.56  0.689

Residual Error  1514  3601.594  2.379

Total                1518  3606.958

Source  DF  Seq SS

income   1   0.443

totexp   1   4.195

age      1   0.080

nk       1   0.647

MTB > let k3 = 5.364/2

MTB > print k3

Data Display

K3    2.68200

Inverse Cumulative Distribution Function

Chi-Square with 2 DF

P( X <= x )        x

       0.95  5.99146

MTB > # since Q=ESS/2 = 2.68200 < chi = 5.99 we have no hetero from Breusch-Pagan Test

Since Q = 2.68200 < 5.99 = 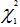, there is sufficient evidence to accept H0 which suggests that there is no heteroscedasticity from the Breusch-Pagan test at 5% significance level which means that one or more slopes are zero.